Problem:
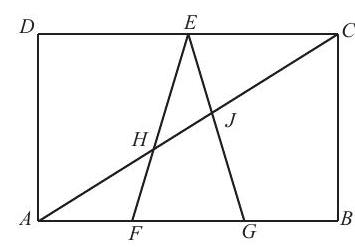
In rectangle ABCD, points F and G lie on AB so that AF=FG=GB and E is the midpoint of DC. Also, AC intersects EF at H and EG at J. The area of rectangle ABCD is 70 . Find the area of triangle EHJ.
Answer Choices:
A. 25
B. 1235
C. 3
D. 27
E. 835
Solution:
The area of triangle EFG is (1/6)(70)=35/3. Triangles AFH and CEH are similar, so 3/2= EC/AF=EH/HF and EH/EF=3/5. Triangles AGJ and CEJ are similar, so 3/4=EC/AG= EJ/JG and EJ/EG=3/7.
Since the areas of the triangles that have a common altitude are proportional to their bases, the ratio of the area of △EHJ to the area of △EHG is 3/7, and the ratio of the area of △EHG to that of △EFG is 3/5. Therefore, the ratio of the area of △EHJ to the area of △EFG is (3/5)(3/7)=9/35. Thus, the area of △EHJ is (9/35)(35/3)=3.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions