Problem:
A semicircle of diameter 1 sits at the top of a semicircle of diameter 2 , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
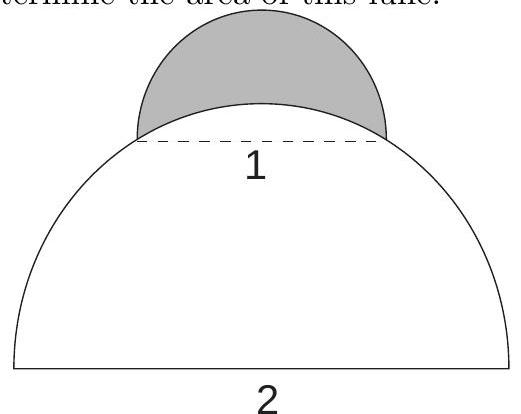
Answer Choices:
A. 61βΟβ43ββ
B. 43βββ121βΟ
C. 43βββ241βΟ
D. 43ββ+241βΟ
E. 43ββ+121βΟ Solution:
First note that the area of the region determined by the triangle topped by the semicircle of diameter 1 is
21ββ 23ββ+21βΟ(21β)2=43ββ+81βΟ
The area of the lune results from subtracting from this the area of the sector of the larger semicircle,
61βΟ(1)2=61βΟ
So the area of the lune is
43ββ+81βΟβ61βΟ=43βββ241βΟβ
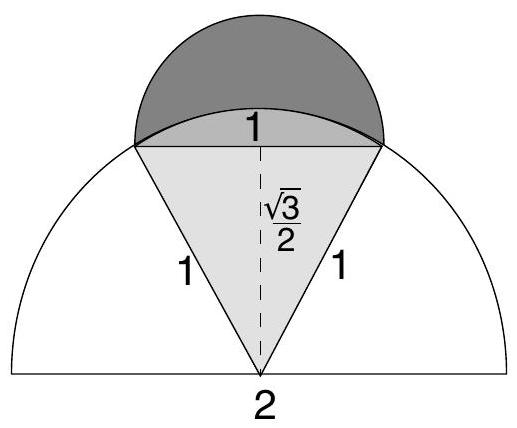
Note that the answer does not depend on the position of the lune on the semicircle.
