Problem:
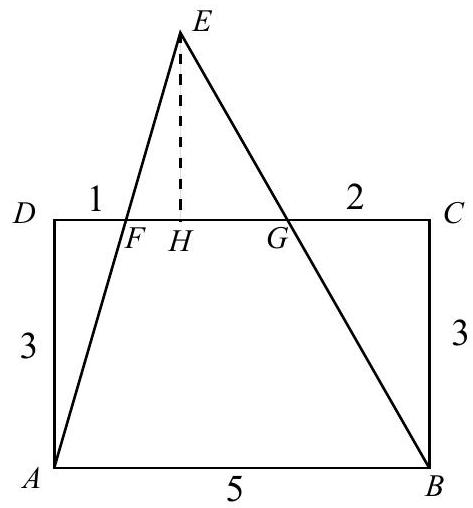
In rectangle ABCD,AB=5 and BC=3. Points F and G are on CD so that DF=1 and GC=2. Lines AF and BG intersect at E. Find the area of △AEB.
Answer Choices:
A. 10
B. 221
C. 12
D. 225
E. 15
Solution:
Let H be the foot of the perpendicular from E to DC. Since CD=AB=5, FG=2, and △FEG is similar to △AEB, we have
EH+3EH=52, so 5EH=2EH+6
and EH=2. Hence
Area(△AEB)=21(2+3)⋅5=225
OR
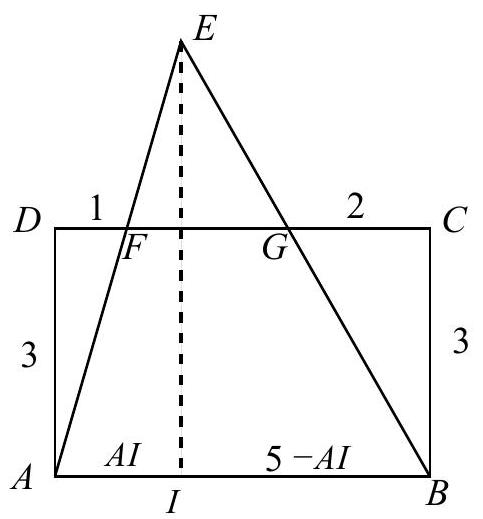
Let I be the foot of the perpendicular from E to AB. Since
△EIA is similar to △ADF and △EIB is similar to △BCG,\
we have
EIAI=31 and EI5−AI=32
Adding gives 5/EI=1, so EI=5. The area of the triangle is 21⋅5⋅5=225.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)