¶ 2003 AMC 12B Problem 15
Problem:
A regular octagon has an area of one square unit. What is the area of the rectangle ?
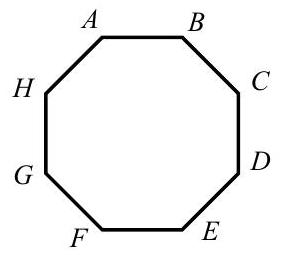
Answer Choices:
A.
B.
C.
D.
E.
Solution:
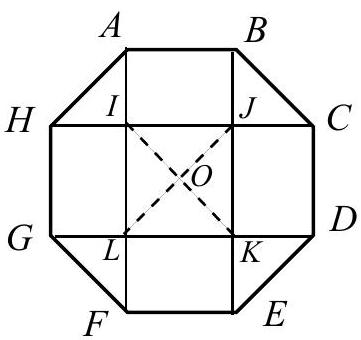
Let be the intersection of the diagonals of . Since the octagon is regular, has area . Since is the midpoint of and have the same area. Thus has area , so has area .
.jpg)
OR
Let be the intersection of the diagonals of the square . Rectangles , and are congruent. Also , so the right isosceles triangles and are congruent. By symmetry, the area in the center square is the sum of the areas of , , and . Thus the area of rectangle is half the area of the octagon.
The problems on this page are the property of the MAA's American Mathematics Competitions