¶ 2003 AMC 12B Problem 22
Problem:
Let be a rhombus with and . Let be a point on , and let and be the feet of the perpendiculars from to and , respectively. Which of the following is closest to the minimum possible value of
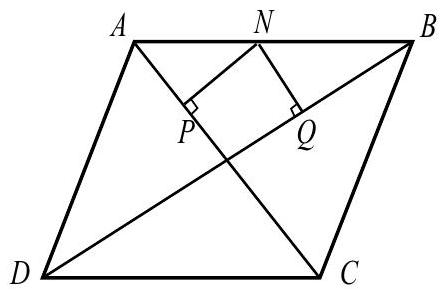
Answer Choices:
A.
B.
C.
D.
E.
Solution:
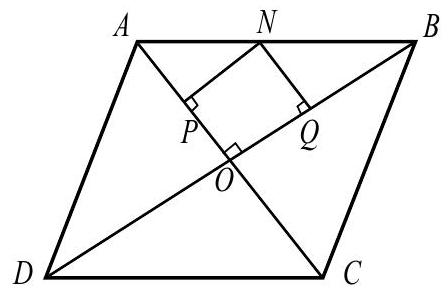
Let be the point of intersection of and . Then is a right triangle with legs and . Quadrilateral is a rectangle because it has right angles at , and . Thus , because the diagonals of a rectangle are of equal length. The minimum value of is the minimum value of . This is achieved if and only if is the foot of the altitude from in triangle . Writing the area of in two different ways yields
Hence the minimum value of is
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions