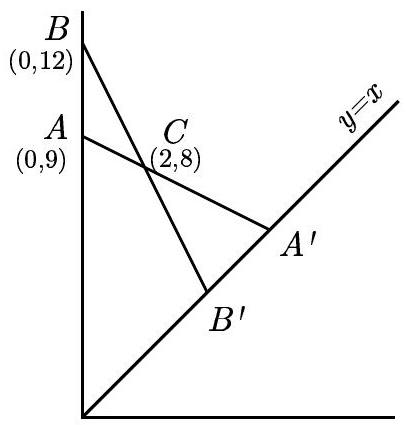
Problem:
Let A=(0,9) and B=(0,12). Points A′ and B′ are on the line y=x, and AA′ and BB′ intersect at C=(2,8). What is the length of A′B′ ?
Answer Choices:
A. 2
B. 22
C. 3
D. 2+2
E. 32
Solution:
Line AC has slope 21 and y-intercept (0,9), so its equation is
y=21x+9
Since the coordinates of A′ satisfy both this equation and y=x, it follows that A′=(6,6). Similarly, line BC has equation y=2x+12, and B′=(4,4). Thus
A′B′=(64)2+(64)2=22
The problems on this page are the property of the MAA's American Mathematics Competitions