¶ 2005 AMC 12A Problem 15
Problem:
Let be a diameter of a circle and be a point on with . Let and be points on the circle such that and is a second diameter. What is the ratio of the area of to the area of
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the center of the circle. Each of and has a diameter of the circle as a side. Thus the ratio of their areas is the ratio of the two altitudes to the diameters. These altitudes are and the altitude from to in . Let be the foot of this second altitude. Since is similar to ,
which is the desired ratio.
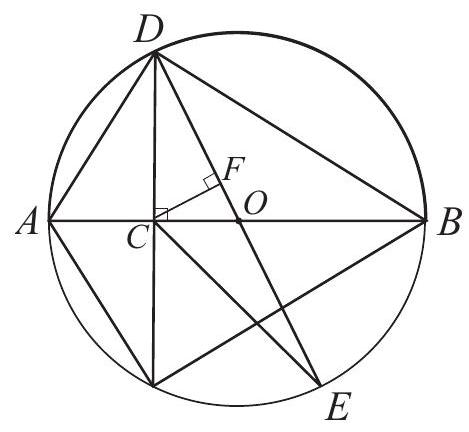
OR
Because and , we have . Triangles and have a common altitude to so the area of is the area of . Triangles and have equal areas since they have a common\
base and their altitudes are equal. Thus the ratio of the area of to the area of is .
The problems on this page are the property of the MAA's American Mathematics Competitions