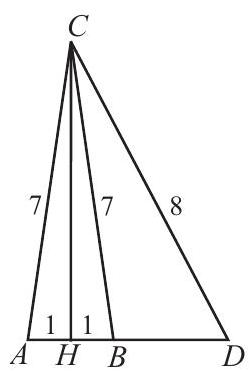
Problem:
In △ABC, we have AC=BC=7 and AB=2. Suppose that D is a point on line AB such that B lies between A and D and CD=8. What is BD ?
Answer Choices:
A. 3
B. 23
C. 4
D. 5
E. 42
Solution:
Let CH be an altitude of △ABC. Applying the Pythagorean Theorem to △CHB and to △CHD produces
82−(BD+1)2=CH2=72−12=48, so (BD+1)2=16
Thus BD=3.
The problems on this page are the property of the MAA's American Mathematics Competitions