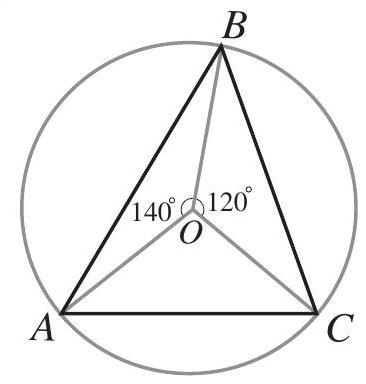
Problem:
The point O is the center of the circle circumscribed about △ABC, with ∠BOC= 120∘ and ∠AOB=140∘, as shown. What is the degree measure of ∠ABC ?
Answer Choices:
A. 35
B. 40
C. 45
D. 50
E. 60
Solution:
Since OA=OB=OC, triangles AOB,BOC, and COA are all isosceles. Hence
∠ABC=∠ABO+∠OBC=2180∘−140∘+2180∘−120∘=50∘
OR
Since
∠AOC=360∘−140∘−120∘=100∘,
the Central Angle Theorem implies that
∠ABC=21∠AOC=50∘.
The problems on this page are the property of the MAA's American Mathematics Competitions