¶ 2008 AMC 12A Problem 12
Problem:
A function has domain and range . (The notation denotes .) What are the domain and range, respectively, of the function defined by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
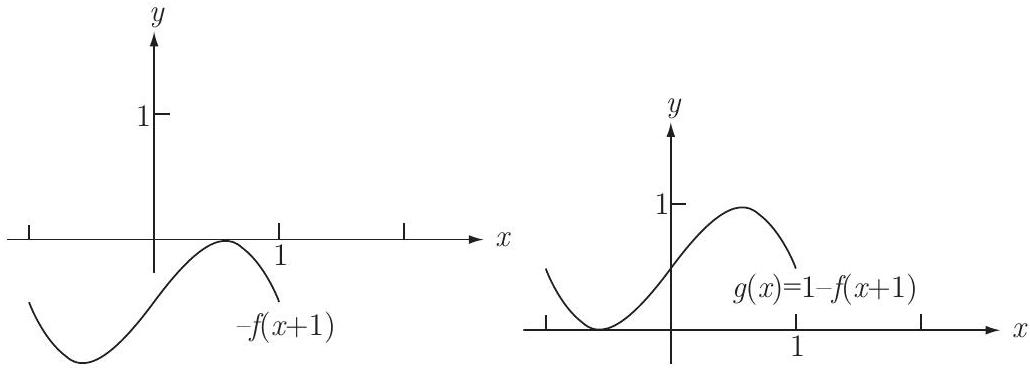
Because the domain of is is defined for , or . Thus is also defined for , so its domain is . Because the range of is , the values of are all the numbers between 0 and 1 , inclusive. Thus the values of are all the numbers between and , inclusive, so the range of is .
OR
.jpg)
The graph of is obtained by shifting the graph of one unit to the left. The graph of is obtained by reflecting the graph of across the -axis. The graph of is obtained by shifting the graph of up one unit. As the figures illustrate, the domain and range of are and , respectively.\
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions