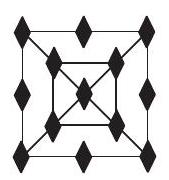
Problem:
The figures F1,F2,F3 and F4 shown are the first in a sequence of figures. For n≥3,Fn is constructed from Fn−1 by surrounding it with a square and placing one more diamond on each side of the new square than Fn−1 had on each side of its outside square. For example, figure F3 has 13 diamonds. How many diamonds are there in figure F20?
F1 F2 F3
Answer Choices:
A. 401
B. 485
C. 585
D. 626
E. 761
Solution:
The outside square for Fn has 4 more diamonds on its boundary than the outside square for Fn−1. Because the outside square of F2 has 4 diamonds, the outside square of Fn has 4(n−2)+4=4(n−1) diamonds. Hence the number of diamonds in figure Fn is the number of diamonds in Fn−1 plus 4(n−1), or
1+4+8+12+⋯+4(n−2)+4(n−1)=1+4(1+2+3+⋯+(n−2)+(n−1))=1+42(n−1)n=1+2(n−1)n.
Therefore figure F20 has 1+2⋅19⋅20=761 diamonds.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)