Problem:
Trapezoid ABCD has AD∥BC,BD=1,∠DBA=23∘, and ∠BDC=46∘. The ratio BC:AD is 9:5. What is CD ?
Answer Choices:
A. 97
B. 54
C. 1513
D. 98
E. 1514
Solution:
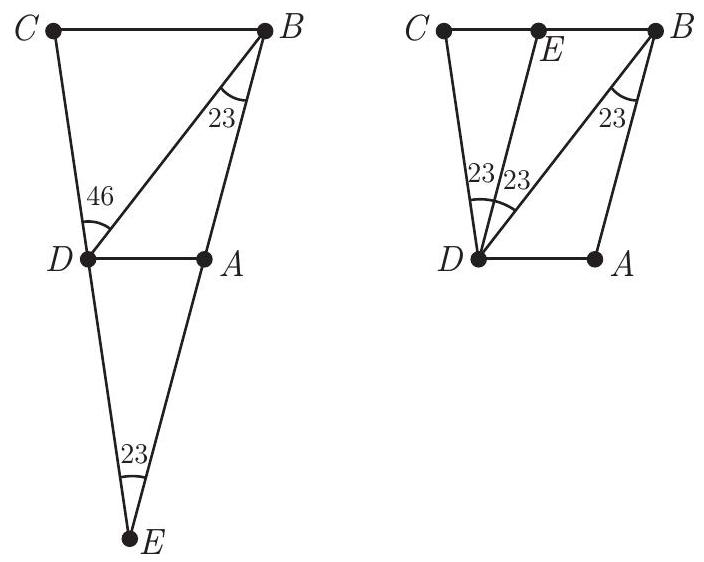
Extend AB and DC to meet at E. Then
∠BED=180∘−∠EDB−∠DBE=180∘−134∘−23∘=23∘.
Thus △BDE is isosceles with DE=BD. Because AD∥BC, it follows that the triangles BCD and ADE are similar. Therefore
59=ADBC=DECD+DE=BDCD+1=CD+1
so CD=54.
\section*{OR}
Let E be the intersection of BC and the line through D parallel to AB. By construction BE=AD and ∠BDE=23∘; it follows that DE is the bisector of the angle BDC. By the Bisector Theorem we get
CD=BDCD=BEEC=BEBC−BE=ADBC−1=59−1=54
The problems on this page are the property of the MAA's American Mathematics Competitions