Problem:
For how many values of x in [0,Ο] is sinβ1(sin6x)=cosβ1(cosx) ? Note: The functions sinβ1=arcsin and cosβ1=arccos denote inverse trigonometric functions.
Answer Choices:
A. 3
B. 4
C. 5
D. 6
E. 7
Solution:
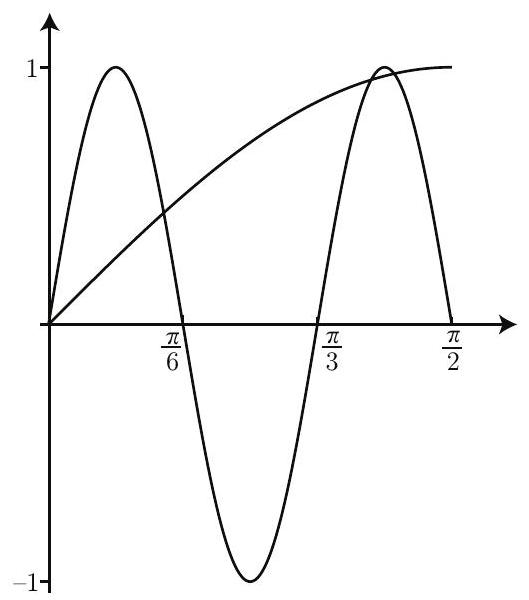
Let f(x)=sinβ1(sin6x) and g(x)=cosβ1(cosx). If 0β€ xβ€Ο, then g(x)=x. If 0β€xβ€Ο/12, then f(x)=6x. Note also that sin(6(6Οββx))=sin6x,sin(6(3Οββx))=βsin6x, and sin(6(3Οβ+x))= sin6x, from which it follows that f(6Οββx)=f(x),f(3Οββx)=βf(x), and f(3Οβ+x)=f(x). Thus the graph of y=f(x) has period 3Οβ and consists of line segments with slopes of 6 or -6 and endpoints at ((4k+1)12Οβ,2Οβ) and ((4k+3)12Οβ,β2Οβ) for integer values of k. The graphs of f and g intersect twice in the interval [0,6Οβ] and twice more in the interval [3Οβ,2Οβ]. If 2Οβ<xβ€Ο, then g(x)=x>2Οβ, so the graphs of f and g do not intersect.
OR
In the range [0,Ο], we have cosβ1(cosx)=x. Since the range of sinβ1x is [β2Οβ,2Οβ], it suffices to solve the equation sinβ1(sin(6x))=x on the interval [0,2Οβ]. Since sinx is one-to-one in [0,2Οβ], we can consider the equivalent equation sin(sinβ1(sin(6x)))=sinx, or sin(6x)=sinx. Let f(x)=sin(6x) and g(x)= sinx. Note that f(0)=0,f(12Οβ)=1,f(4Οβ)=β1,f(125Οβ)=1, and f(2Οβ)=0. Moreover f(x) is increasing on (0,12Οβ) and (4Οβ,125Οβ), and decreasing on (12Οβ,4Οβ) and (125Οβ,2Οβ). Similarly g(0)=0,g(2Οβ)=1, and g(x) is increasing on [0,2Οβ]. Thus the graphs of y=f(x) and y=g(x) intersect at x=0, once in the interval [12Οβ,4Οβ], once in the interval [4Οβ,125Οβ], and once more in the interval [125Οβ,2Οβ]. Therefore there are 4β solutions to the given equation.
The problems on this page are the property of the MAA's American Mathematics Competitions
