Problem:
Circles with radii 1,2 , and 3 are mutually externally tangent. What is the area of the triangle determined by the points of tangency?
Answer Choices:
A. 53
B. 54
C. 1
D. 56
E. 34
Solution:
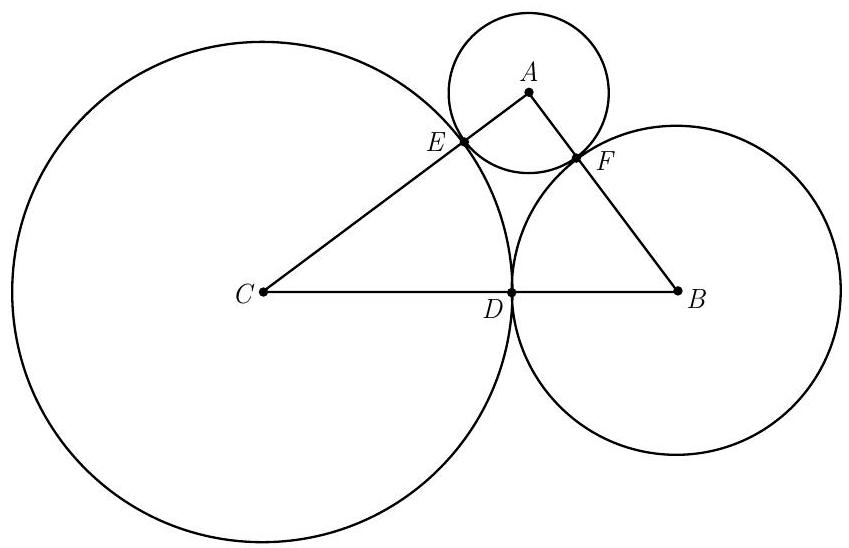
Let A,B, and C be the centers of the circles with radii 1,2 , and 3 , respectively. Let D,E, and F be the points of tangency, where D is on the circles B and C,E is on the circles A and C, and F is on the circles A and B. Because AB=AF+FB=1+2=3,BC=BD+DC=2+3=5, and CA=CE+EA=3+1=4, it follows that △ABC is a 3-4-5 right triangle. Therefore
[ABC]=21AB⋅AC=6,[AEF]=21AE⋅AF=21[BFD]=21BD⋅BF⋅sin(∠FBD)=21⋅2⋅2⋅54=58, and [CDE]=21CD⋅CE⋅sin(∠DCE)=21⋅3⋅3⋅53=1027
Hence
[DEF]=[ABC]−[AEF]−[BFD]−[CDE]
=6−21−58−1027=56
The problems on this page are the property of the MAA's American Mathematics Competitions