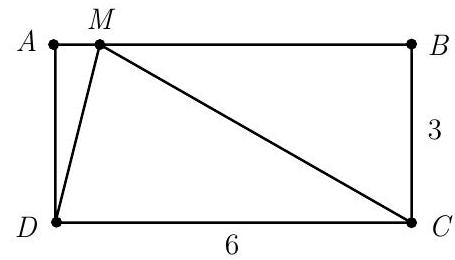
Problem:
Rectangle ABCD has AB=6 and BC=3. Point M is chosen on side AB so that ∠AMD=∠CMD. What is the degree measure of ∠AMD ?
Answer Choices:
A. 15
B. 30
C. 45
D. 60
E. 75
Solution:
Sides AB and CD are parallel, so ∠CDM=∠AMD. Because ∠AMD=∠CMD, it follows that △CMD is isosceles and CD=CM=6. Therefore △MCB is a 30−60−90∘ right triangle with ∠BMC=30∘. Finally, 2⋅∠AMD+30∘=∠AMD+∠CMD+30∘=180∘, so ∠AMD=75∘.
The problems on this page are the property of the MAA's American Mathematics Competitions