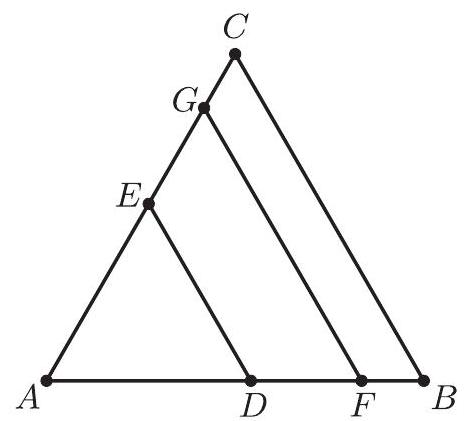
Problem:
Triangle ABC is equilateral with AB=1. Points E and G are on AC and points D and F are on AB such that both DE and FG are parallel to BC. Furthermore, triangle ADE and trapezoids DFGE and FBCG all have the same perimeter. What is DE+FG ?
Answer Choices:
A. 1
B. 23
C. 1321
D. 813
E. 35
Solution:
Let x=DE and y=FG. Then the perimeter of ADE is x+x+x=3x, the perimeter of DFGE is x+(y−x)+y+(y−x)=3y−x, and the perimeter of FBCG is y+(1−y)+1+(1−y)=3−y. Because the perimeters are equal, it follows that 3x=3y−x=3−y. Solving this system yields x=139 and y=1312. Thus DE+FG=x+y=1321.
The problems on this page are the property of the MAA's American Mathematics Competitions