¶ 2013 AMC 12A Problem 13
Problem:
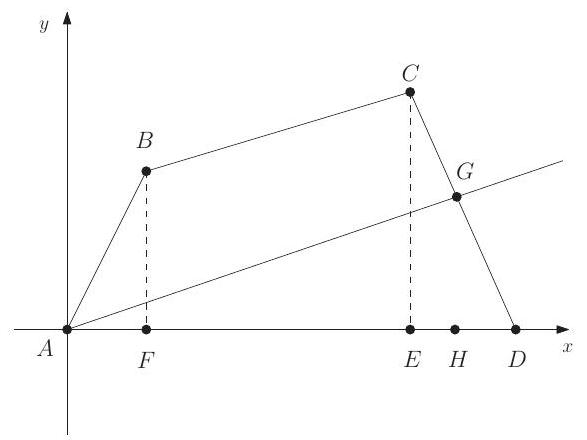
Let points , and . Quadrilateral is cut into equal area pieces by a line passing through . This line intersects at point , where these fractions are in lowest terms. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let line be the required line, with on . Divide into triangle , trapezoid , and triangle , as shown. Their areas are 1,5 , and , respectively. Hence the area of , and the area of triangle . Because , it follows that . The equation of is , so when . Therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions