Problem:
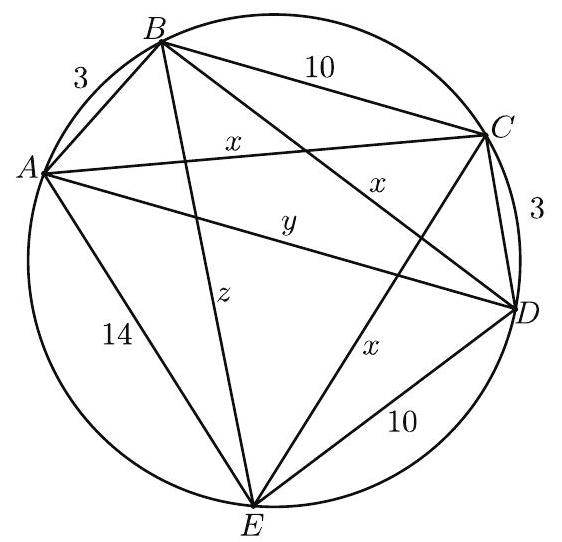
Let ABCDE be a pentagon inscribed in a circle such that AB=CD=3, BC=DE=10, and AE=14. The sum of the lengths of all diagonals of ABCDE is equal to nm, where m and n are relatively prime positive integers. What is m+n ?
Answer Choices:
A. 129
B. 247
C. 353
D. 391
E. 421
Solution:
Let x=AC,y=AD, and z=BE. Because the arcsABC, BCD, and CDE are congruent, it follows that AC=BD=CE=x.
By Ptolemy's Theorem applied to the quadrilaterals ABCD,ABDE, and BCDE, it follows that
10y+9=x2,30+14x=yz, and 100+3z=x2
Solving for y and z in the first and third equations and substituting in the second equation gives
30+14x=(10x2−9)(3x2−100)=30x4−109x2+900,
which implies that
900+420x=x4−109x2+900.
Thus x3−109x−420=0. This equation factors as (x−12)(x+5)(x+7)=0. Because x>0 it follows that x=12,y=101(x2−9)=10135=227, and z= 31(x2−100)=344. The required sum of diagonals equals 3x+y+z=6385, so m+n=385+6=391.
The problems on this page are the property of the MAA's American Mathematics Competitions