¶ 2016 AMC 12B Problem 10
Problem:
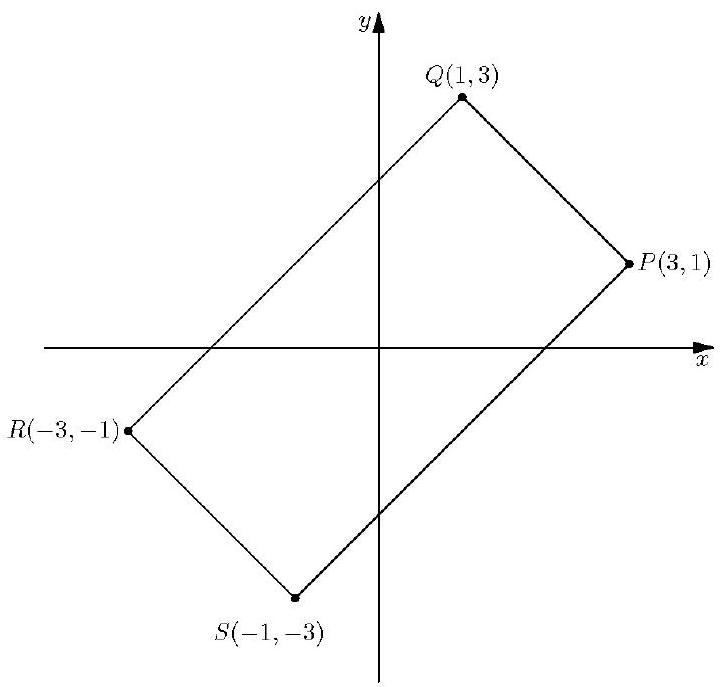
A quadrilateral has vertices , and , where and are integers with . The area of is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The slopes of and are -1 , and the slopes of and are 1 , so the figure is a rectangle. The side lengths are and , so the area is . Therefore . The only perfect squares whose difference is 8 are 9 and 1 , so , , and .
The problems on this page are the property of the MAA's American Mathematics Competitions