¶ 2016 AMC 12B Problem 11
Problem:
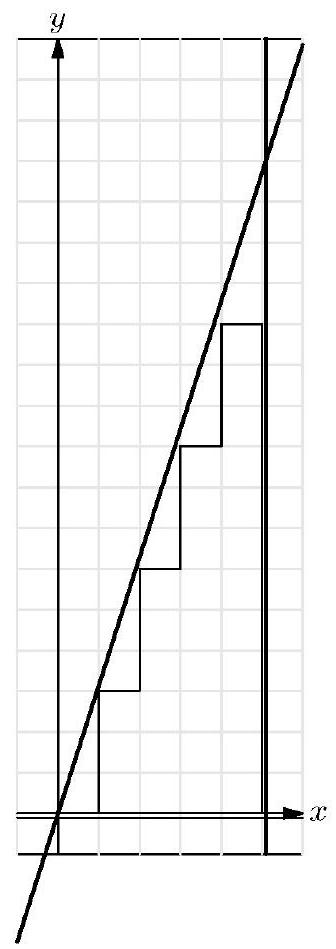
How many squares whose sides are parallel to the axes and whose vertices have coordinates that are integers lie entirely within the region bounded by the line , the line , and the line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that , and . Therefore there are 31 -by-1 squares of the desired type in the strip -by- 1 squares in the strip -by-1 squares in
the strip , and 121 -by- 1 squares in the strip . Furthermore there are 22 -by- 2 squares in the strip -by-2 squares in the strip , and 82 -by-2 squares in the strip . There is 1 3 -by-3 square in the strip , and there are 43 -by-3 squares in the strip . There are no 4 -by- 4 or larger squares. Thus in all there are squares of the desired type within the given region.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions