Problem:
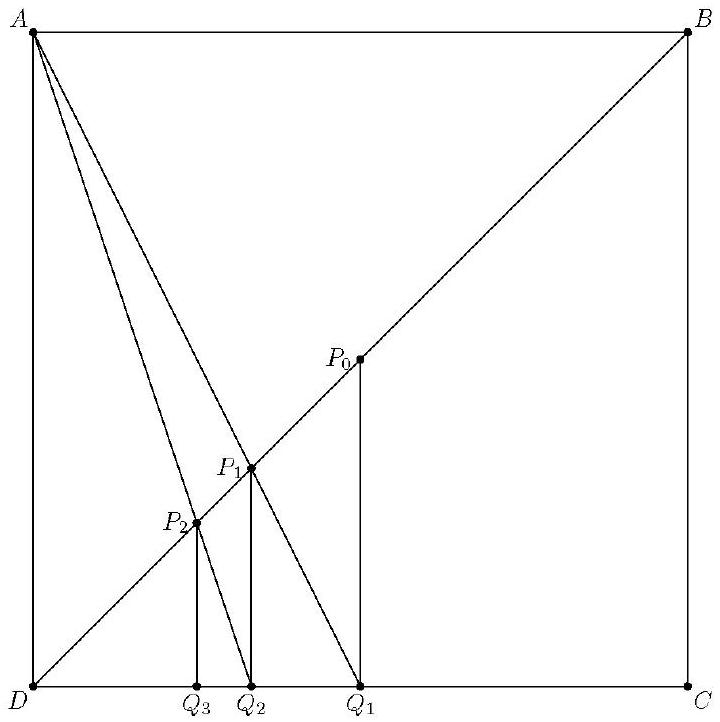
Let ABCD be a unit square. Let Q1 be the midpoint of CD. For i=1,2,…, let Pi be the intersection of AQi and BD, and let Qi+1 be the foot of the perpendicular from Pi to CD. What is
i=1∑∞ Area of △DQiPi?
Answer Choices:
A. 61
B. 41
C. 31
D. 21
E. 1
Solution:
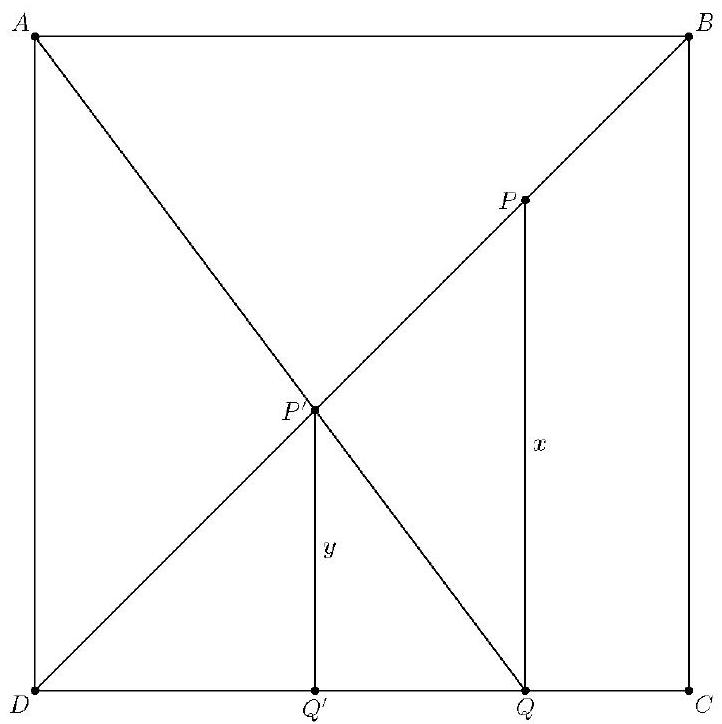
For any point P between B and D, let Q be the foot of the perpendicular from P to CD, let P′ be the intersection of AQ and BD, and let Q′ be the foot of the perpendicular from P′ to CD. Let x=PQ and y=P′Q′. Because △PQD and △P′Q′D are isosceles right triangles, DQ=x and DQ′=y. Because △ADQ is similar to △P′Q′Q,x1=x−yy. Solving for y gives y=1+xx.
Now let $P_{0}$ be the midpoint of $\overline{B D}$. Then $P_{0} Q_{1}=D Q_{1}=\dfrac{1}{2}$. It follows from the analysis above that $P_{1} Q_{2}=D Q_{2}=\dfrac{1}{3}, P_{2} Q_{3}=D Q_{3}=\dfrac{1}{4}$, and in general $P_{i} Q_{i+1}=D Q_{i+1}=\dfrac{1}{i+2}$. The area of $\triangle D Q_{i} P_{i}$ is
21⋅DQi⋅PiQi+1=21⋅i+11⋅i+21=21(i+11−i+21).
The requested infinite sum telescopes:
i=1∑∞ Area of △DQiPi=21(21−31+31−41+41−51+⋯)
Its value is 21⋅21=41.
The problems on this page are the property of the MAA's American Mathematics Competitions