Problem:
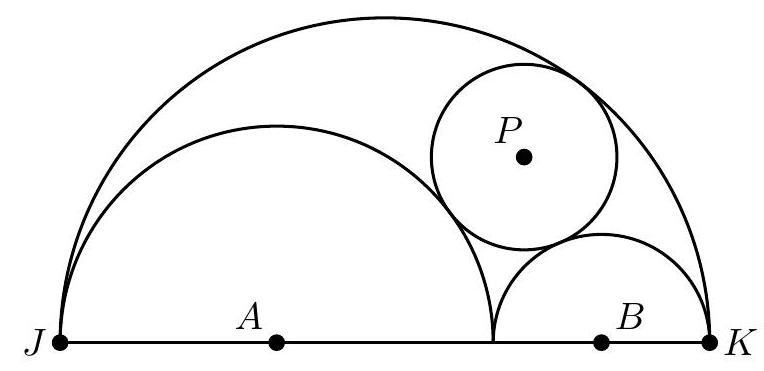
In the figure below, semicircles with centers at A and B and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter JK. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at P is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at P?
Answer Choices:
A. 43β
B. 76β
C. 21β3β
D. 85β2β
E. 1211β Solution:
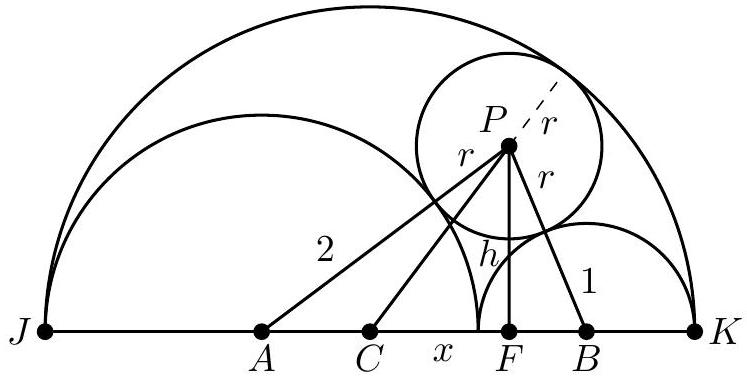
Let C be the center of the largest semicircle, and let r denote the radius of the circle centered at P. Note that PA=2+r, PC=3βr,PB=1+r,AC=1,BC=2, and AB=3. Let F be the foot of the perpendicular from P to AB, let h=PF, and let x=CF. The Pythagorean Theorem in β³PAF,β³PCF, and β³PBF gives
This reduces to two linear equations in r and x, whose solution is r=76β,x=79β.
OR
With the notation and observations above, apply Heron's Formula to β³PCB and β³PAC, noting that the former has twice the area of the latter and each has semiperimeter 3 . Thus
3β 1β rβ (rβ2)β=23β 2β rβ (rβ1)β
from which it follows that r=76ββ.
OR
With the notation and observations above, let ΞΈ=β PAB. The Law of Cosines applied to β³PAC gives
(3βr)2=(2+r)2+12β2β (2+r)β 1β cosΞΈ
and simplifying yields (2+r)cosΞΈ=5rβ2. Applying the Law of Cosines to β³PAB gives
(1+r)2=(2+r)2+32β2β (2+r)β 3β cosΞΈ
and simplifying yields 3(2+r)cosΞΈ=r+6. Hence r+6=3(5rβ2), so r=76ββ.
