¶ 2018 AMC 12A Problem 18
Problem:
Triangle with and has area 120 . Let be the midpoint of , and let be the midpoint of . The angle bisector of intersects and at and , respectively. What is the area of quadrilateral
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Because is of , it follows from the Angle Bisector Theorem that is of , and is of . Because trapezoids and have the same height, the area of is of the area of . Furthermore, the area of is of the area of , so its area is 30 , and the area of trapezoid is . Therefore the area of quadrilateral is .
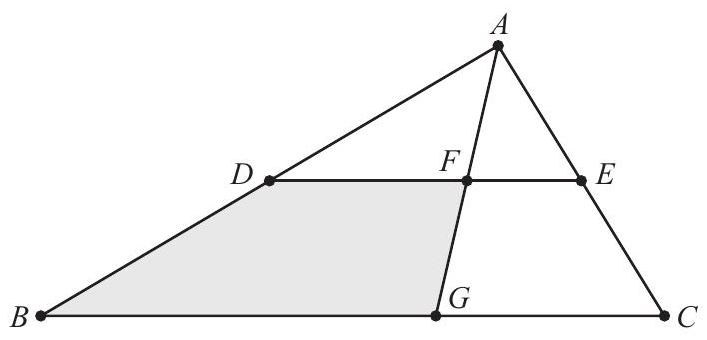
Note: The figure (not drawn to scale) shows the situation in which is acute. In this case and . It is also possible for to be obtuse, with and . These values can be calculated using the Law of Cosines and the sine formula for area.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions