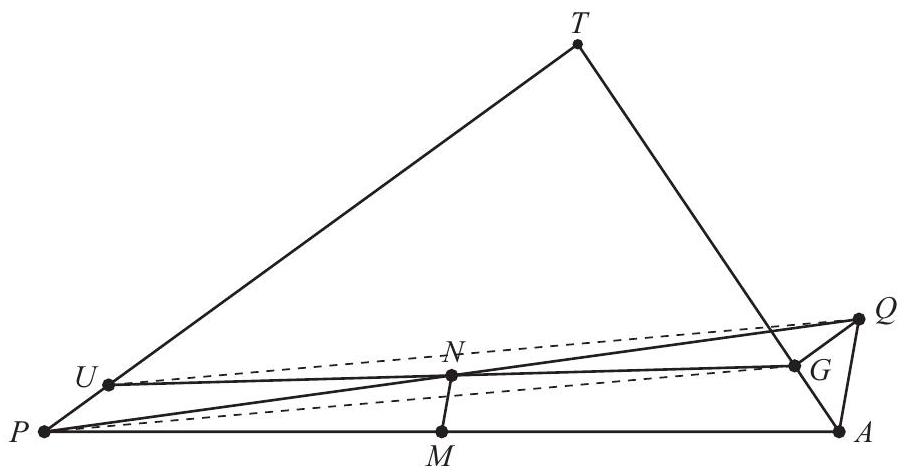
Problem:
In △PAT,∠P=36∘,∠A=56∘, and PA=10. Points U and G lie on sides TP and TA, respectively, so that PU=AG=1. Let M and N be the midpoints of segments PA and UG, respectively. What is the degree measure of the acute angle formed by lines MN and PA?
Answer Choices:
A. 76
B. 77
C. 78
D. 79
E. 80
Solution:
Extend PN through N to Q so that PN=NQ. Segments UG and PQ bisect each other, implying that UPGQ is a parallelogram. Therefore GQ∥PT, so ∠QGA=180∘−∠T= ∠TPA+∠TAP=36∘+56∘=92∘. Furthermore GQ=PU=AG, so △QGA is isosceles, and ∠QAG=21(180∘−92∘)=44∘. Because MN is a midline of △QPA, it follows that MN∥AQ and
∠NMP=∠QAP=∠QAG+∠GAP=44∘+56∘=100∘,
so acute ∠NMA=80∘. (Note that the value of the common length PU=AG is immaterial.)
OR
Place the figure in the coordinate plane with P=(−5,0),M=(0,0), A=(5,0), and T in the first quadrant. Then
U=(−5+cos36∘,sin36∘) and G=(5−cos56∘,sin56∘)
and the midpoint N of UG is
(21(cos36∘−cos56∘),21(sin36∘+sin56∘)).
The tangent of ∠NMA is the slope of line MN, which is calculated as follows using the sum-to-product trigonometric identites:
tan(∠NMA)=cos36∘−cos56∘sin36∘+sin56∘=−2sin236∘+56∘sin236∘−56∘2sin236∘+56∘cos236∘−56∘=sin10∘cos10∘=cot10∘=tan80∘
and it follows that ∠NMA=80∘.
The problems on this page are the property of the MAA's American Mathematics Competitions