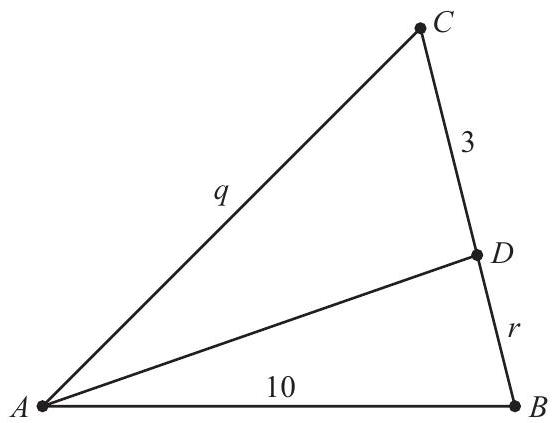
Problem:
Side AB of △ABC has length 10 . The bisector of angle A meets BC at D, and CD=3. The set of all possible values of AC is an open interval (m,n). What is m+n ?
Answer Choices:
A. 16
B. 17
C. 18
D. 19
E. 20
Solution:
Let q=AC and r=BD. By the Angle Bisector Theorem,
CDAC=BDAB, which means 3q=r10, so r=q30
The possible values of AC can be determined by considering the three Triangle Inequalities in △ABC.
-
AC+BC>AB, which means q+3+r>10. Substituting for r and simplifying gives q2−7q+30>0, which always holds because q2−7q+30=(q−27)2+471.
-
BC+AB>AC, which means 3+r+10>q. Substituting r=q30, simplifying, and factoring gives (q−15)(q+2)<0, which holds if and only if −2<q<15.
-
AB+AC>BC, which means 10+q>3+r. Substituting r=q30, simplifying, and factoring gives (q+10)(q−3)>0, which holds if and only if q>3 or q<−10.
Combining these inequalities shows that the set of possible values of q is the open interval (3,15), and the requested sum of the endpoints of the interval is 3+15=18.
The problems on this page are the property of the MAA's American Mathematics Competitions