Problem:
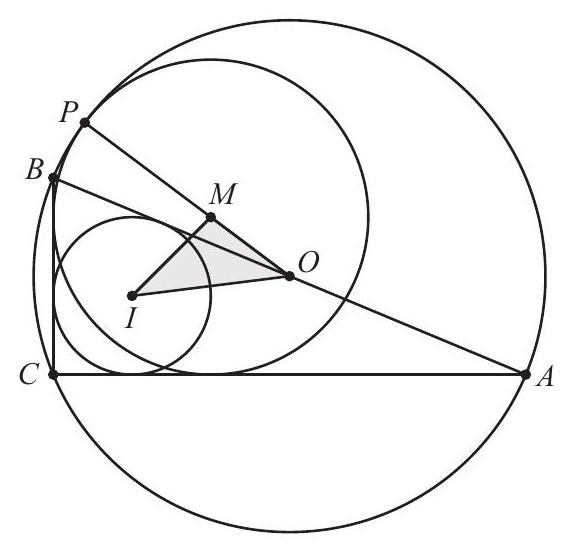
In β³ABC with side lengths AB=13,AC=12, and BC=5, let O and I denote the circumcenter and incenter, respectively. A circle with center M is tangent to the legs AC and BC and to the circumcircle of β³ABC. What is the area of β³MOI ?
Answer Choices:
A. 25β
B. 411β
C. 3
D. 413β
E. 27β Solution:
Place the figure on coordinate axes with coordinates A(12,0),B(0,5), and C(0,0). The center of the circumscribed circle is the midpoint of the hypotenuse of right triangle ABC, so the coordinates of O are (6,25β). The radius r of the inscribed circle equals the area of the triangle divided by its semiperimeter, which here is 30Γ·15=2, so the center of the inscribed circle is I(2,2). Because the circle with center M is tangent to both coordinate axes, its center has coordinates (Ο,Ο), where Ο is its radius. Let P be the point of tangency of this circle and the circumscribed circle. Then M,P, and O are collinear because MP and OP are perpendicular to the common tangent line at P. Thus MO=OPβMP=213ββΟ. By the distance formula, MO=(Οβ6)2+(Οβ25β)2β. Equating these expressions and solving for Ο shows that Ο=4. The area of β³MOI can now be computed using the shoelace formula:
Alternatively, the area can be computed as 21β times MI, which by the distance formula is (4β2)2+(4β2)2β=22β, times the distance from point O to the line MI, whose equation is xβy+0=0. This last value is
