¶ 2018 AMC 12B Problem 23
Problem:
Ajay is standing at point near Pontianak, Indonesia, latitude and longitude. Billy is standing at point near Big Baldy Mountain, Idaho, USA, latitude and longitude. Assume that Earth is a perfect sphere with center . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
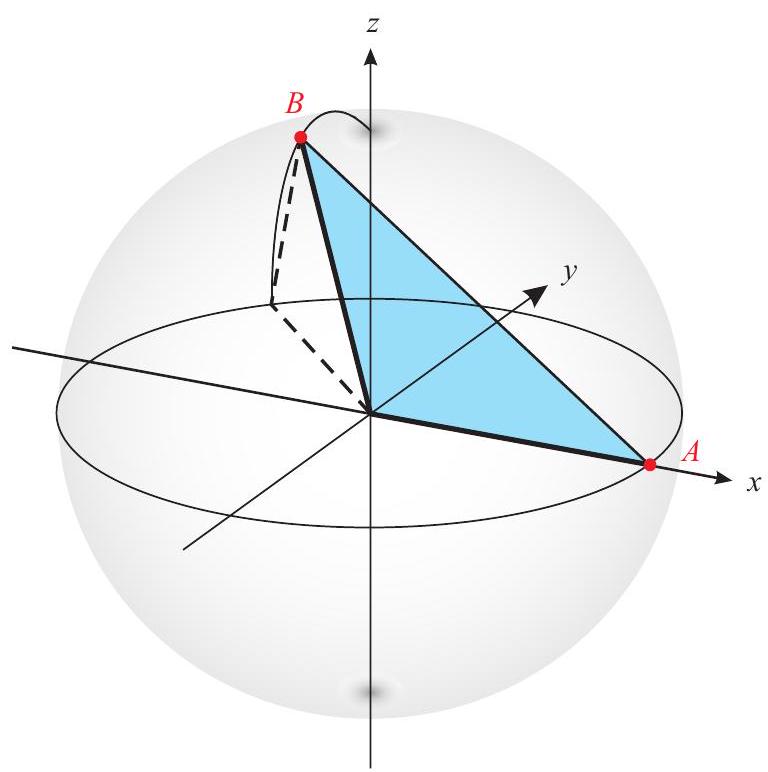
To travel from to , one could circle east along the equator and then north. Construct an coordinate system with origin at Earth's center , the positive -axis running through , the positive -axis running through the equator at west longitude, and the positive -axis running through the North Pole. Set Earth's radius to be 1 . The coordinates of are . Let be the -coordinate of ; note that . Then the -coordinate of will be , and the -coordinate will be . Because the distance from the center of Earth is 1,
so , and the coordinates are . The distance is therefore
Applying the Law of Cosines to gives
so and . An alternative to using the Law of Cosines to find is to compute the dot product of the unit vectors and .
The problems on this page are the property of the MAA's American Mathematics Competitions