Problem:
Let ⌊x⌋ denote the greatest integer less than or equal to x. How many real numbers x satisfy the equation x2+10,000⌊x⌋=10,000x ?
Answer Choices:
A. 197
B. 198
C. 199
D. 200
E. 201
Solution:
Let {x}=x−⌊x⌋ denote the fractional part of x. Then 0≤{x}<1. The given equation is equivalent to x2= 10,000{x}, that is,
10,000x2={x}
Therefore if x satisfies the equation, then
0≤10,000x2<1
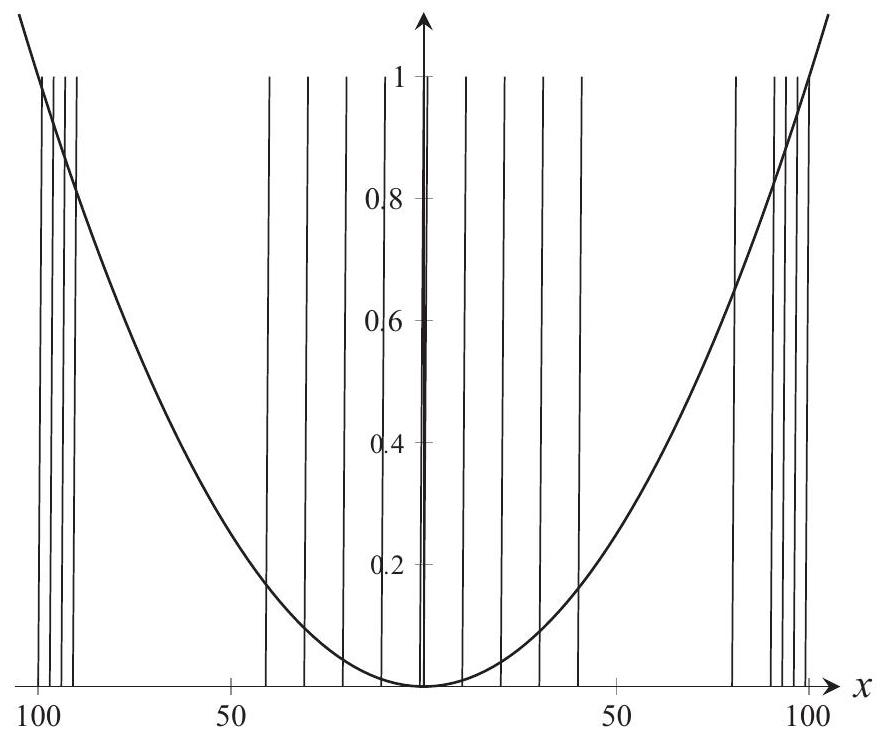
This implies that x2<10,000, so −100<x<100. The figure shows a sketch of the graphs of
f(x)=10,000x2 and g(x)={x}
for −100<x<100 on the same coordinate axes. The graph of g consists of the 200 half-open line segments with slope 1 connecting the points (k,0) and (k+1,1) for k=−100,−99,…,98,99. (The endpoints of these intervals that lie on the x-axis are part of the graph, but the endpoints with y-coordinate 1 are not.) It is clear that there is one intersection point for x lying in each of the intervals [−100,−99), [−99,−98),[−98,−97),…,[−1,0),[0,1),[1,2),…,[97,98),[98,99) but no others. Thus the equation has 199 solutions.
OR
The solutions to the equation correspond to points of intersection of the graphs y=10000⌊x⌋ and y=10000x−x2. There will be a point of intersection any time the parabola intersects the half-open horizontal segment from the point (a,10000a) to the point (a+1,10000a), where a is an integer. This occurs for every integer value of a for which
10000a−a2≤10000a<10000(a+1)−(a+1)2
This is equivalent to (a+1)2<10000, which occurs if and only if −101<a<99. Thus points of intersection occur on the intervals [a,a+1) for a=−100,−99,−98,…,−1,0,1,…,97,98, resulting in 199 points of intersection.
The problems on this page are the property of the MAA's American Mathematics Competitions