Problem:
Let Ο=β21β+21βi3β. Let S denote all points in the complex plane of the form a+bΟ+cΟ2, where 0β€aβ€1,0β€bβ€1, and 0β€cβ€1. What is the area of S ?
Answer Choices:
A. 21β3β
B. 43β3β
C. 23β3β
D. 21βΟ3β
E. Ο Solution:
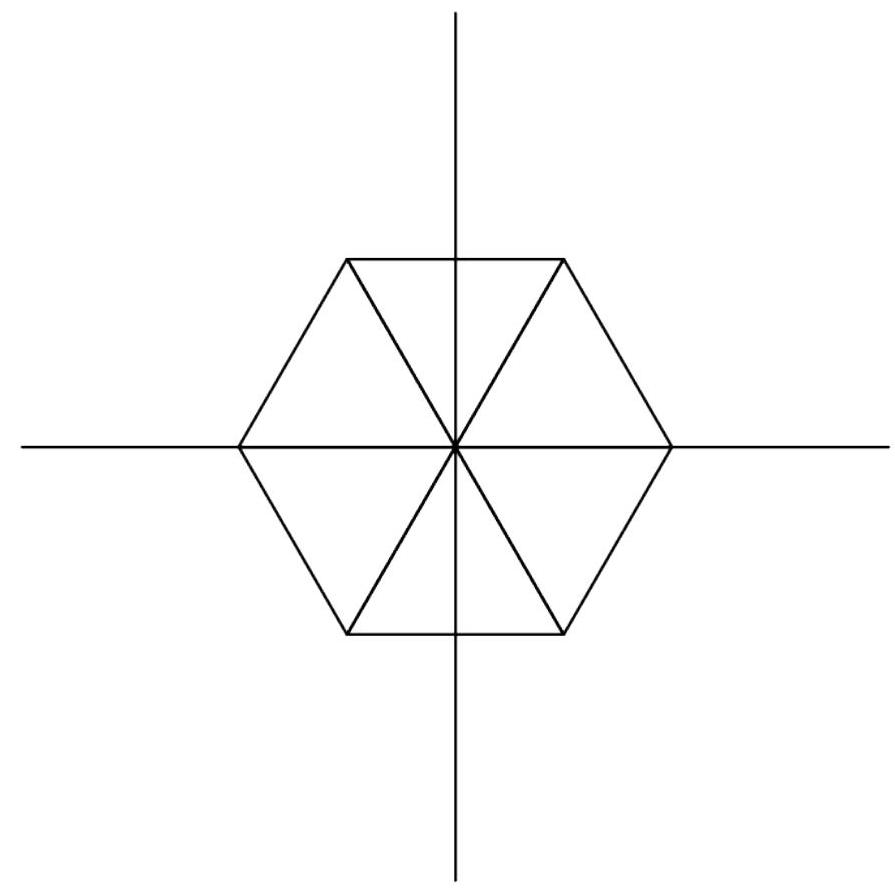
Notice that Ο=e32iΟβ, which is one of the cube roots of unity. We wish to find the span of (a+bΟ+cΟ2) for reals 0β€a,b,cβ€1. Observe also that if a,b,c>0, then replacing a,b, and c by aβmin(a,b,c),bβmin(a,b,c), and cβmin(a,b,c) leaves the value of a+bΟ+cΟ2 unchanged. Therefore, assume that at least one of a,b,c is equal to 0 . If exactly one of them is 0 , we can form an equilateral triangle of side length 1 using the remaining terms. A similar argument works if exactly two of them are 0 . In total, we get 3+(23β)=6 equilateral triangles, whose total area is 6β 43ββ=(C)23β3ββ.
Note: A diagram of the six equilateral triangles is shown below.
