¶ 2020 AMC 12A Problem 12
Problem:
Line in the coordinate plane has the equation . This line is rotated counterclockwise about the point to obtain line . What is the -coordinate of the intercept of line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
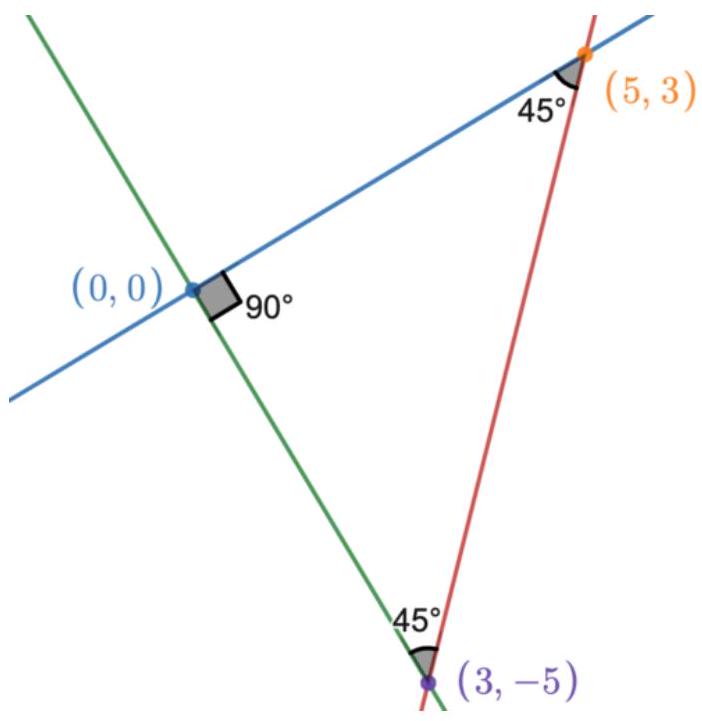
The slope of the line is . We must transform it by .
creates an isosceles right triangle, since the sum of the angles of the triangle must be and one angle is . This means the last leg angle must also be .
In the isosceles right triangle, the two legs are congruent. We can therefore construct an isosceles right triangle with a line of slope on graph paper. That line with slope starts at and will go to , the vector .
Construct another line from to , the vector . This is and equal to the original line segment. The difference between the two vectors is , which is the slope , and that is the slope of line .
Furthermore, the equation passes straight through since , which means that any rotations about would contain . We can create a line of slope through . The -intercept is therefore .
OR
Since the slope of the line is , and the angle we are rotating around is , then
Hence, the slope of the rotated line is . Since we know the line intersects the point , then we know the line is . Set to find the -intercept, and so .
The problems on this page are the property of the MAA's American Mathematics Competitions