¶ 2020 AMC 12A Problem 18
Problem:
Quadrilateral satisfies , and . Diagonals and intersect at point , and . What is the area of quadrilateral ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
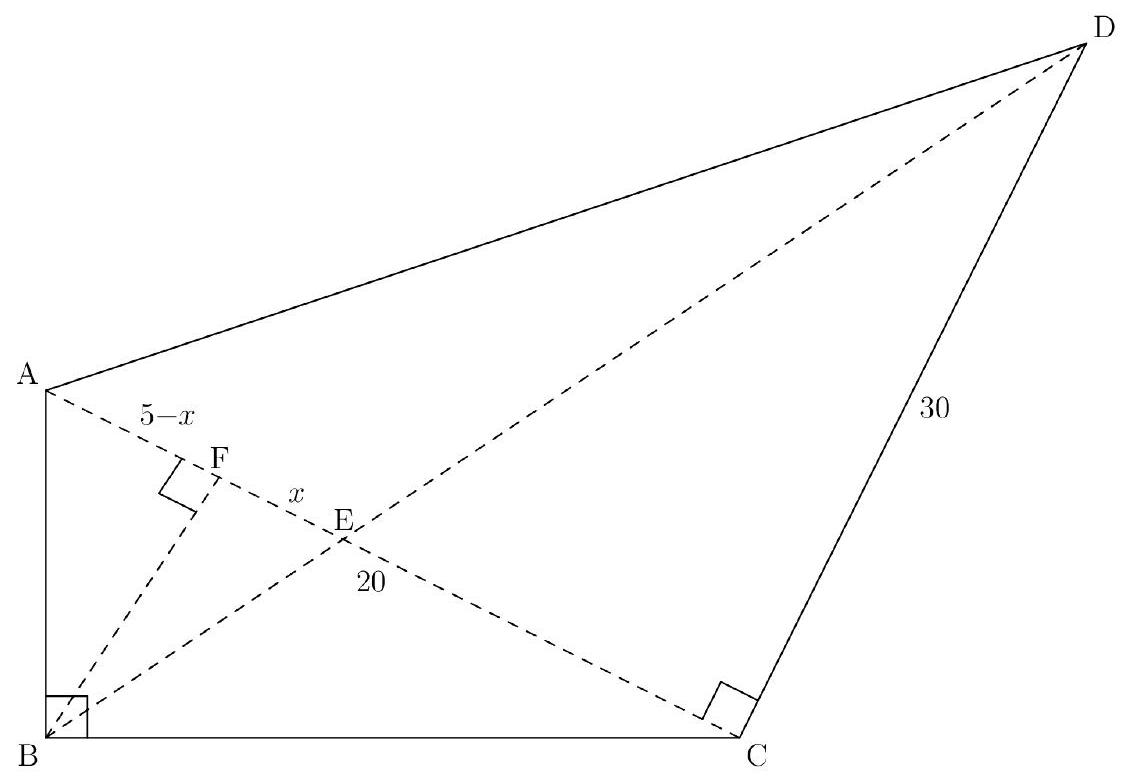
It's crucial to draw a good diagram for this one. Since and , we get . Now we need to find to get the area of the whole quadrilateral. Drop an altitude from to and call the point of intersection . Let . Since , then .
By dropping this altitude, we can also see two similar triangles, . Since is , and , we get that .
Now, if we redraw another diagram just of , we get that because of the altitude geometric mean theorem which states that in any right triangle, the altitude squared is equal to the product of the two lengths that it divides the base into.
Expanding, simplifying, and dividing by the GCF, we get . This factors to , which has roots of . Since lengths cannot be negative, . Since , that means the altitude , or . Thus
OR
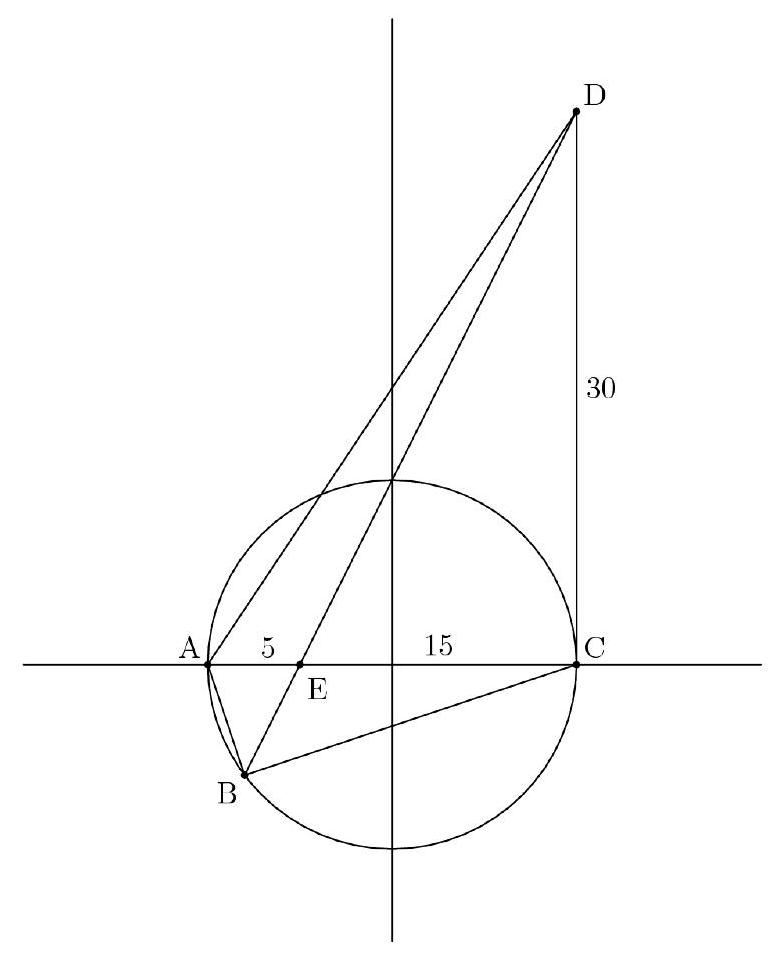
Let the points be , and , respectively. Since lies on line , we know that . Furthermore, since lies on the circle with diameter , so . Solving for and with these equations, we get the solutions and . We immediately discard the solution as should be negative. Thus, we conclude that .
The problems on this page are the property of the MAA's American Mathematics Competitions