Problem:
How many solutions does the equation tan(2x)=cos(2xβ) have on the interval [0,2Ο] ?
Answer Choices:
A. 1
B. 2
C. 3
D. 4
E. 5
Solution:
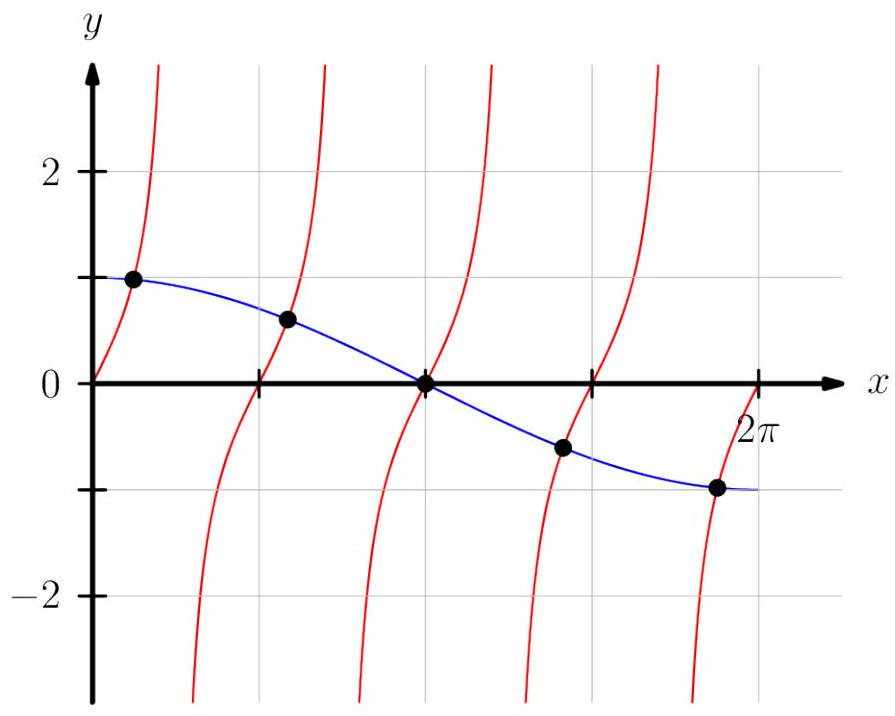
Solution We count the intersections of the graphs of y=tan(2x) and y=cos(2xβ) :
The graph of y=tan(2x) has a period of 2Οβ, asymptotes at x=4Οβ+2kΟβ, and zeros at x=2kΟβ for some integer k. On the interval [0,2Ο], the graph has five branches:
[0,4Οβ),(4Οβ,43Οβ),(43Οβ,45Οβ),(45Οβ,47Οβ),(47Οβ,2Ο]
Note that tan(2x)β[0,β) for the first branch, tan(2x)β(ββ,β) for the three middle branches, and tan(2x)β (ββ,0] for the last branch. Moreover, all branches are strictly increasing.
The graph of y=cos(2xβ) has a period of 4Ο and zeros at x=Ο+2kΟ for some integer k. On the interval [0,2Ο], note that cos(2xβ)β[β1,1]. Moreover, the graph is strictly decreasing.
The graphs of y=tan(2x) and y=cos(2xβ) intersect once on each of the five branches of y=tan(2x), as shown below:
y=tan(2x)
y=cos(2xβ)
Therefore, the answer is (E)5β .
The problems on this page are the property of the MAA's American Mathematics Competitions
