¶ 2020 AMC 12B Problem 18
Problem:
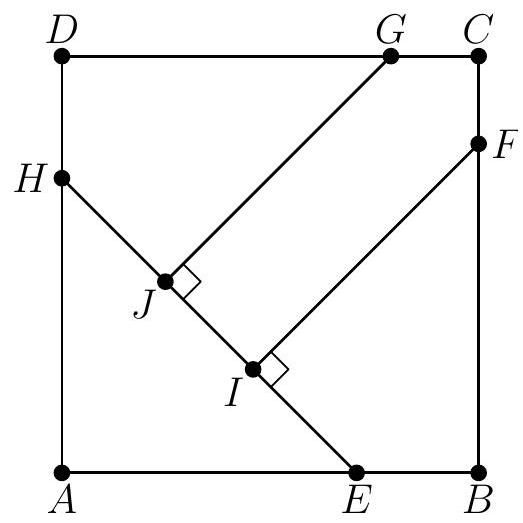
In square , points and lie on and , respectively, so that . Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral , quadrilateral , and pentagon each has area 1 . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Since the total area is , the side length of square is . We see that since triangle is a right isosceles triangle with area , we can determine sides and both to be . Now, consider extending and until they intersect. Let the point of intersection be . We note that is also a right isosceles triangle with side and find its area to be . Now, we notice that is also a right isosceles triangle (because ) and find it's area to be . This is also equal to or . Since we are looking for , we want two times this. That gives .
OR
Draw the auxiliary line . Denote by the point it intersects with , and by the point it intersects with . Last, denote by the segment , and by the segment . We will find two equations for and , and then solve for .
Since the overall area of is , and . In addition, the area of .
The two equations for and are then:
Length of
Area of CMIF: .
Substituting the first into the second, yields
Solving for gives .
The problems on this page are the property of the MAA's American Mathematics Competitions