¶ Spring 2021 AMC 12A Problem 21
Problem:
The five solutions to the equation
may be written in the form for , where and are real. Let be the unique ellipse that passes through the points , and . The eccentricity of can be written in the form where and are relatively prime positive integers. What is ? (Recall that the eccentricity of an ellipse is the ratio , where is the length of the major axis of and is the is the distence between its two foci.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The solutions to this equation are , and . Consider the five points , and . These are five points that lie on . Note that because these five points are symmetric about the -axis, must also have this property. Therefore the equation of the ellipse is of the form
which is equivalent to
where the center of the ellipse is at with is the length of the semi-major axis, and is the length of the semi-minor axis (or vice versa, but it will it turn out that ).
Evaluating at the point yields . Evaluating at the points and yields the equations
Multiplying the first equation by -2 and the second equation by 3 and then adding leads to , so . It then follows from either of the above equations that . Note that , as promised. Letting denote the distance from the center of the ellipse to a focus, and using the fact that for an ellipse, it follows that . Then the eccentricity of the ellipse is , and therefore .
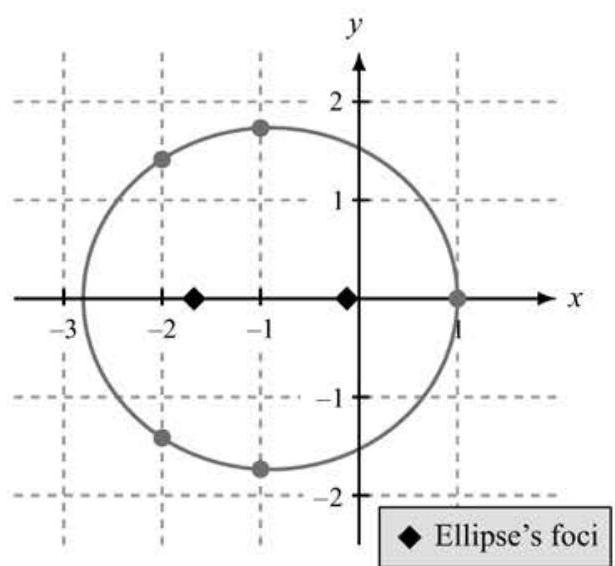
The graph of the ellipse is shown below, with the foci marked.
The problems on this page are the property of the MAA's American Mathematics Competitions