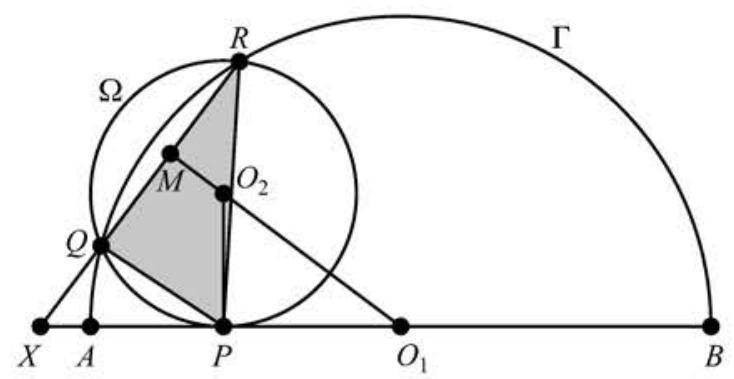
Problem: Γ Γ A B ‾ A B Ω Ω A B ‾ A B P P Γ Γ Q Q R R Q R = 3 3 Q R = 3 3 ∠ Q P R = 6 0 ∘ ∠ Q P R = 6 0 ∘ △ P Q R △ P Q R a b c c a b a a c c b b a + b + c a + b + c
Answer Choices:
A. 110 1 1 0 114 1 1 4 118 1 1 8 122 1 2 2 126 1 2 6 Solution:
Let O 1 O 1 O 2 O 2 Γ Γ Ω Ω Q R Q R A B A B X X Q Q X X R R
[ △ P Q R ] = [ △ X P R ] − [ △ X P Q ] = 1 2 ⋅ X P ⋅ X R ⋅ sin ( ∠ P X Q ) − 1 2 ⋅ X P ⋅ X Q ⋅ sin ( ∠ P X Q ) = 1 2 ⋅ X P ⋅ Q R ⋅ sin ( ∠ P X Q ) , [ △ P Q R ] = [ △ X P R ] − [ △ X P Q ] = 2 1 ⋅ X P ⋅ X R ⋅ sin ( ∠ P X Q ) − 2 1 ⋅ X P ⋅ X Q ⋅ sin ( ∠ P X Q ) = 2 1 ⋅ X P ⋅ Q R ⋅ sin ( ∠ P X Q ) ,
where the brackets indicate area. Let M M Q R ‾ Q R O 1 O 2 O 1 O 2
Triangle Q O 2 R Q O 2 R 3 3 3 3 12 0 ∘ 1 2 0 ∘ O 2 M = 3 2 O 2 M = 2 3 O 2 Q = O 2 R = 3 O 2 Q = O 2 R = 3
O 1 M = ( O 1 Q ) 2 − ( M Q ) 2 = 7 2 − ( 3 3 2 ) 2 = 13 2 O 1 M = ( O 1 Q ) 2 − ( M Q ) 2 = 7 2 − ( 2 3 3 ) 2 = 2 1 3
so
O 1 O 2 = O 1 M − O 2 M = 13 2 − 3 2 = 5 O 1 O 2 = O 1 M − O 2 M = 2 1 3 − 2 3 = 5
Hence O 1 P = ( O 1 O 2 ) 2 − ( O 2 P ) 2 = 5 2 − 3 2 = 4 O 1 P = ( O 1 O 2 ) 2 − ( O 2 P ) 2 = 5 2 − 3 2 = 4
The similarity △ X M O 1 ∼ △ O 2 P O 1 △ X M O 1 ∼ △ O 2 P O 1
sin ( ∠ P X Q ) = sin ( ∠ P O 2 O 1 ) = 4 5 , sin ( ∠ P X Q ) = sin ( ∠ P O 2 O 1 ) = 5 4 ,
so
O 1 X = O 1 M sin ( ∠ P X Q ) = 13 2 ÷ 4 5 = 65 8 . O 1 X = sin ( ∠ P X Q ) O 1 M = 2 1 3 ÷ 5 4 = 8 6 5 .
Therefore
X P = O 1 X − O 1 P = 65 8 − 4 = 33 8 X P = O 1 X − O 1 P = 8 6 5 − 4 = 8 3 3
so
[ △ P Q R ] = 1 2 ⋅ X P ⋅ Q R ⋅ sin ( ∠ P X Q ) = 1 2 ⋅ 33 8 ⋅ 3 3 ⋅ 4 5 = 99 3 20 . [ △ P Q R ] = 2 1 ⋅ X P ⋅ Q R ⋅ sin ( ∠ P X Q ) = 2 1 ⋅ 8 3 3 ⋅ 3 3 ⋅ 5 4 = 2 0 9 9 3 .
The requested sum is 99 + 3 + 20 = 122 9 9 + 3 + 2 0 = 1 2 2
The problems on this page are the property of the MAA's American Mathematics Competitions