¶ Spring 2021 AMC 12B Problem 15
Problem:
The figure below is constructed from 11 line segments, each of which has length 2 . The area of pentagon can be written as , where and are positive integers. What is ?
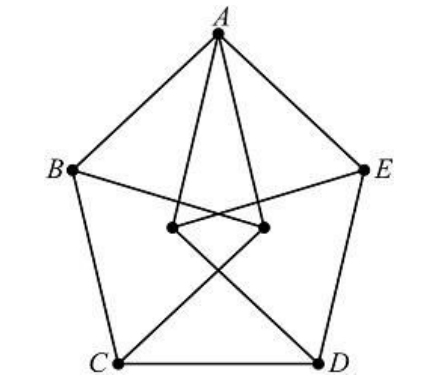
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Answer (D): Let be the midpoint of , and label the remaining points and as shown in the diagram below.
Observe that
where the brackets denote area. Because the four equilateral triangles have side length 2 , their areas are each. The sum is equal to the combined areas of two of these triangles and hence is equal to . To compute , observe that the triangle is isosceles with and
Then , so . Therefore
so .
OR
Because has twice the length of the median of an equilateral triangle of side 2 , its length is , and the solution proceeds as above.
Note: This configuration is referred to as the Moser spindle. It is a unit-distance graph with chromatic number 4.
The problems on this page are the property of the MAA's American Mathematics Competitions