¶ 2022 AMC 12A Problem 13
Problem:
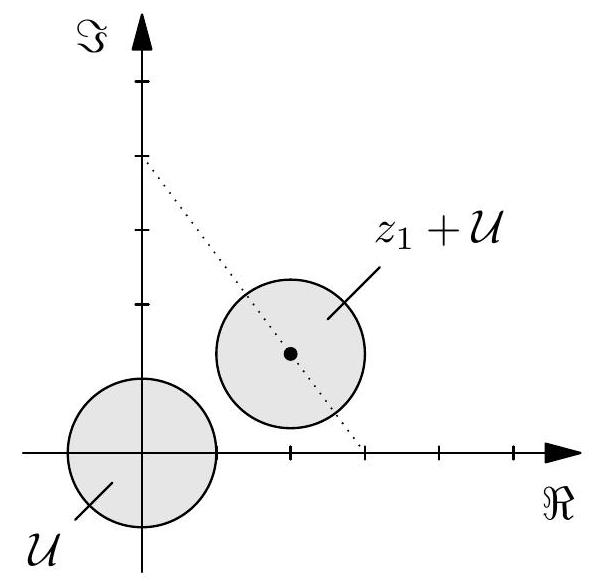
Let be the region in the complex plane consisting of all complex numbers that can be written as the sum of complex numbers and , where lies on the segment with endpoints 3 and , and has magnitude at most . What integer is closest to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The set of complex numbers with is the unit disc centered at the origin. For any given , the set of complex numbers , for all in , is the unit disc centered at . Translating the unit disc centered at along the line segment from to sweeps out the region . Thus consists of a rectangular region sandwiched between two semicircular regions with radius 1 . Two sides of the rectangle are the two diameters of the two semicircular regions; each has length 2 . The other two sides of the rectangle are the two exterior common tangent segments of the two semicircles, and their length is equal to the distance between the two centers of the semicircles, which is . Hence the area of is equal to , and the requested closest integer is .
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions