¶ 2022 AMC 12A Problem 25
Problem:
A circle with integer radius is centered at . Distinct line segments of length connect points to for and are tangent to the circle, where , and are all positive integers and . What is the ratio for the least possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Points ( 0,0 ), ( ), and are the vertices of a right triangle whose sides have integer lengths. Such triangles are called Pythagorean triangles. A circle inside the triangle and tangent to all three sides is called an incircle. A circle outside the triangle, tangent to one side and to extensions of the other two sides is called an excircle. Notice that the 14 Pythagorean triangles being sought will come in pairs. If , and form a suitable triangle, so do , , and . The circle can be either an incircle or an excircle tangent to the hypotenuse of each triangle.
Consider a right triangle with sides and and hypotenuse and with incircle of radius . It will be useful to relate to the side lengths of the triangle. Let be the area of the triangle. Then . Connecting the vertices of the triangle to the center point of the circle divides it into three smaller triangles with base lengths , and and altitude . The sum of the areas of the three smaller triangles is . Equating the two expressions for and solving for gives . If, instead, the circle is an excircle tangent to the hypotenuse, the same construction shows the area of the triangle to be , and .
The problem calls for 14 right triangles whose side lengths , and are related to by one of these two equations. The smallest Pythagorean triangle has , and . The excircle tangent to its hypotenuse has radius
A second solution is obtained by exchanging the lengths and to get a 4-3-5 triangle. Circles with cannot be excircles to Pythagorean triangles.
When the circle is inside the triangle, the shortest side of the triangle must be greater than in order that the other two sides enclose the circle. The shortest side must be no longer than the equal sides of an isosceles right triangle enclosing the same circle; otherwise it would not be shortest. This isosceles triangle has altitude , so its equal sides are . This limits the shortest side of the triangle to be an integer in the range . The number of integers in this range is at most . In order to potentially have at least 12 Pythagorean triangles (six pairs) with incircle of radius , it is necessary that , which implies .
Of course not every integer in the range will be part of a Pythagorean triangle. By Euclid's Formula, the sides of every Pythagorean triangle can be expressed as for some positive integers , and with . Putting these values into the expression for and simplifying gives . Only three triples of values for give , namely , and . Therefore not enough Pythagorean triangles have incircles of radius .
For there are more possibilities for , , and . Some of these duplicate each other, but they generate the following 12 ordered triples of side lengths for right triangles with incircles of radius 6 : , ,, and . Together with the 2 triangles with excircles, these give the required 14 tangent lines; see the figure.
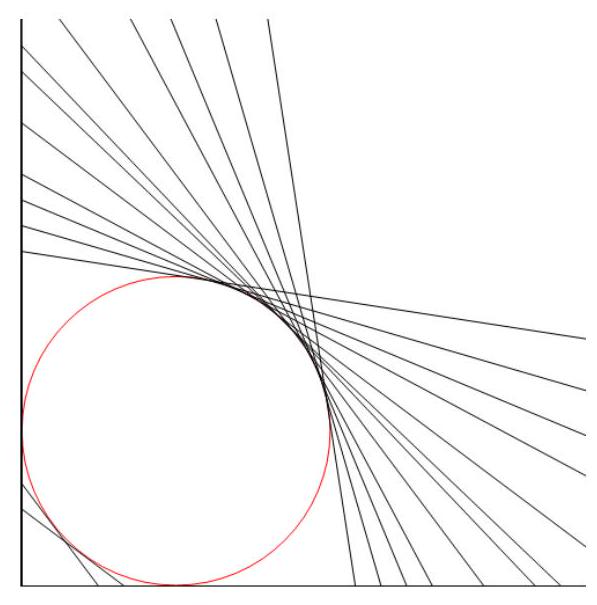
Thus 14 Pythagorean triangles have hypotenuse tangent to the circle of radius 6 . The greatest of the hypotenuse lengths is 85 , and the least is 5 . The requested ratio is .
The problems on this page are the property of the MAA's American Mathematics Competitions