¶ 2022 AMC 12A Problem 3
Problem:
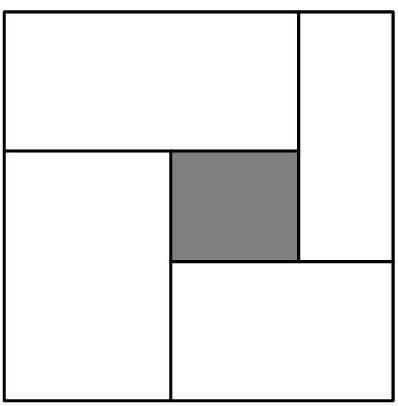
Five rectangles, , and , are arranged in a square as shown below. These rectangles have dimensions , and , respectively. (The figure is not drawn to scale.) Which of the five rectangles is the shaded one in the middle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Observe that the total area of all rectangles, and hence the area of the square, is . This means the side of the large square has length 8 . Therefore the rectangle (rectangle ) must appear on the perimeter of the square, because the side of length 7 is too long to appear in the middle of the square.
By rotating and reflecting the diagram, assume that appears in the top left corner of the square as shown below. The only rectangle with a side of length 1 is rectangle , which must now appear in the top right corner. This leaves the rectangle (rectangle ) to appear in the bottom left corner and the rectangle (rectangle ) to appear in the bottom right corner. From here rectangle slots neatly into the center. The diagram shows that everything fits.
.jpg)
As above, the side length of the square is 8 units. If a side of length 4 is placed along a side of the square, then there must be two rectangles with a side of length 4 to cover all 8 units on that side. But there is only one, namely rectangle . Therefore must be the shaded middle square.
The problems on this page are the property of the MAA's American Mathematics Competitions