¶ 2022 AMC 12A Problem 5
Problem:
The taxicab distance between points and in the coordinate plane is given by
For how many points with integer coordinates is the taxicab distance between and the origin less than or equal to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The points that are taxicab distance from the origin form a diamond shape, as shown below, rather than a circle, as is the case with the usual distance function. There are such points with integer coordinates when and 1 such point when .
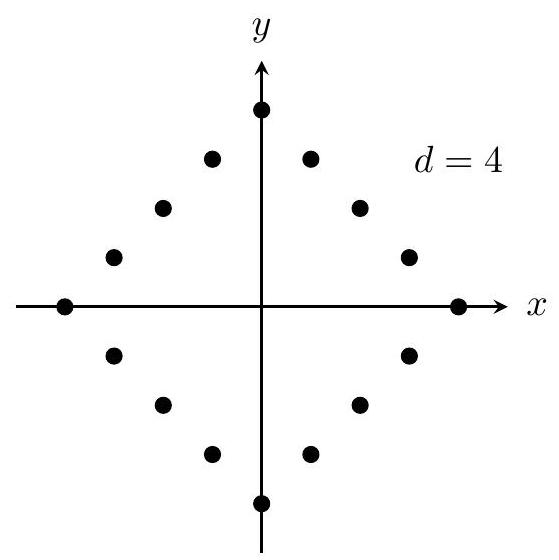
Therefore the number of such points within 20 units of the origin is
In each of the four quadrants, there are
points with integer coordinates within taxicab units of the origin. On each of the signed coordinate axes, not including the origin, there are integer points. Including the origin, there are a total of
such points. Substituting gives .
Counting the number of points within 20 taxicab units of the origin on the lines for gives the total number of points as
This is the sum of the first 21 odd positive integers plus the sum of the first 20 odd positive integers. This sum is equal to .
Note: The notion of distance can be generalized to what is known as the distance (or Minkowski distance) using the formula
The usual Euclidean distance and the taxicab distance are the cases and , respectively. It can be applied to -dimensional space, not just 2 -dimensional space, and there is even a sense in which makes sense.
The problems on this page are the property of the MAA's American Mathematics Competitions