¶ 2025 AMC 12A Problem 14
Problem:
Points and are collinear with between and . The ellipse with foci at and is internally tangent to the ellipse with foci at and , as shown below.
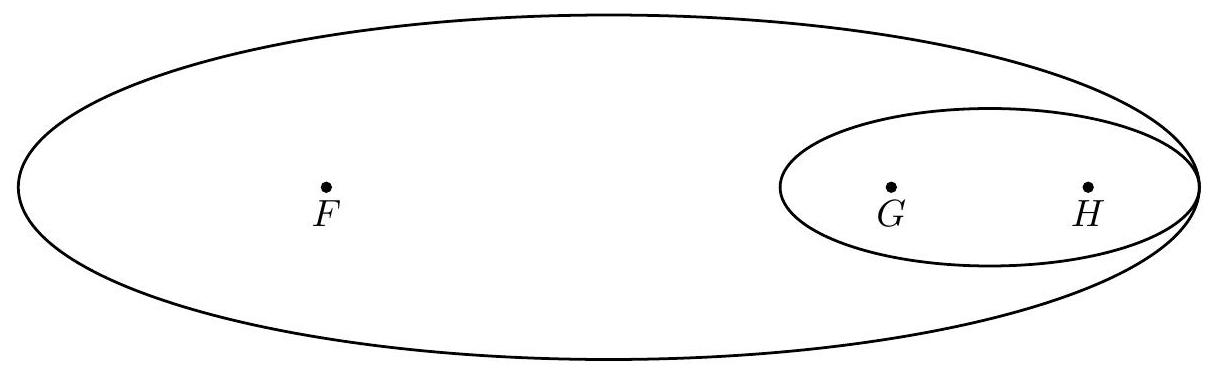
The two ellipses have the same eccentricity , and the ratio of their areas is . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the intersection (or tangency) point of the two circles.
Note that the ellipses are similar - in fact, consider the dilation at that maps the larger ellipse to the smaller ellipse. It must preserve foci, so it must map to and to .
This means that
or .
If we let and be defined as in the problem for the larger ellipse, we get and .
Furthermore, since the ellipses are similar, is a scaled down version of , with ratio (the ratio of areas of similar figures is the square of the ratio of their lengths).
Hence, we get
or
so , or .
The problems on this page are the property of the MAA's American Mathematics Competitions