¶ 2025 AMC 12A Problem 20
Problem:
The base of the pentahedron shown below is a rectangle, and its lateral faces are two isosceles triangles with base and congruent sides , and two isosceles trapezoids with bases and and nonparallel sides .
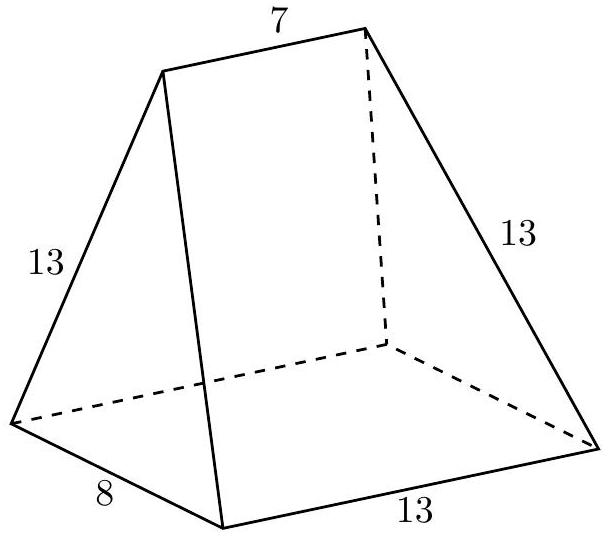
What is the volume of the pentahedron?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First, we split the pentahedron into a pyramid and an oblique trianglular prism by drawing parallel lines as follows:
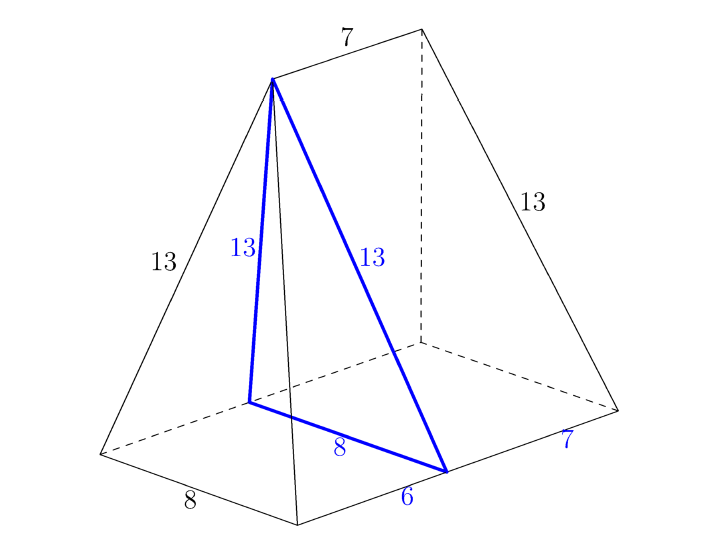
Consider the pyramid on the left. The distance from the center of the rectangular base to its corners is , so its height is and its volume is . Now, we will transform the oblique triangular prism on the right. Note that the triangular prism formed by the red planes in the diagram below must have the same volume as the original one, since all we have down is shift volume from the right to the left.
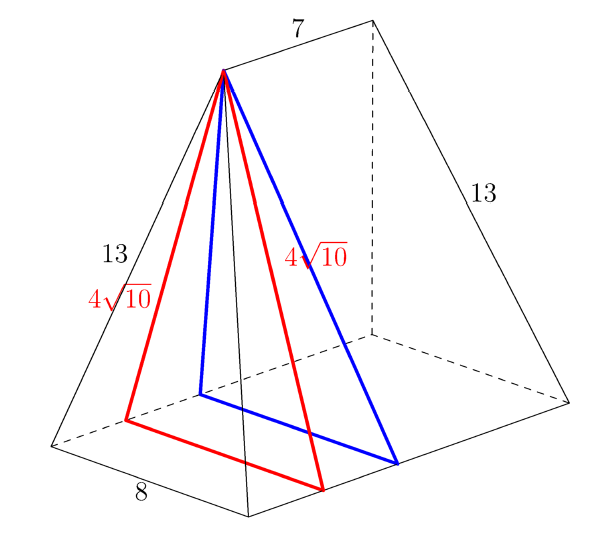
To calculate the volume of this new prism, note that the side lengths are by the . This has height and area , so the red triangles have area . The height of the prism is , and so its volume is .
Hence, the final volume is .
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions