¶ 2025 AMC 12A Problem 24
Problem:
A circle of radius is surrounded by circles of radius , externally tangent to the central circle and sequentially tangent to each other, as shown. Then can be written as , where are integers. What is
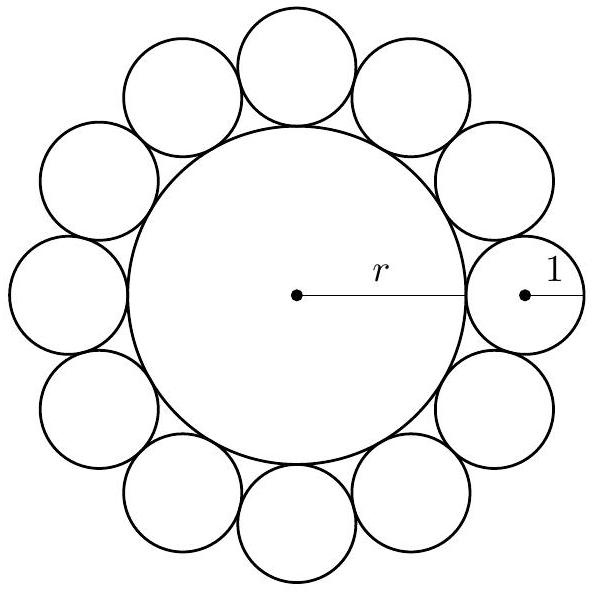
Answer Choices:
A.
B.
C.
D.
E.
Solution:
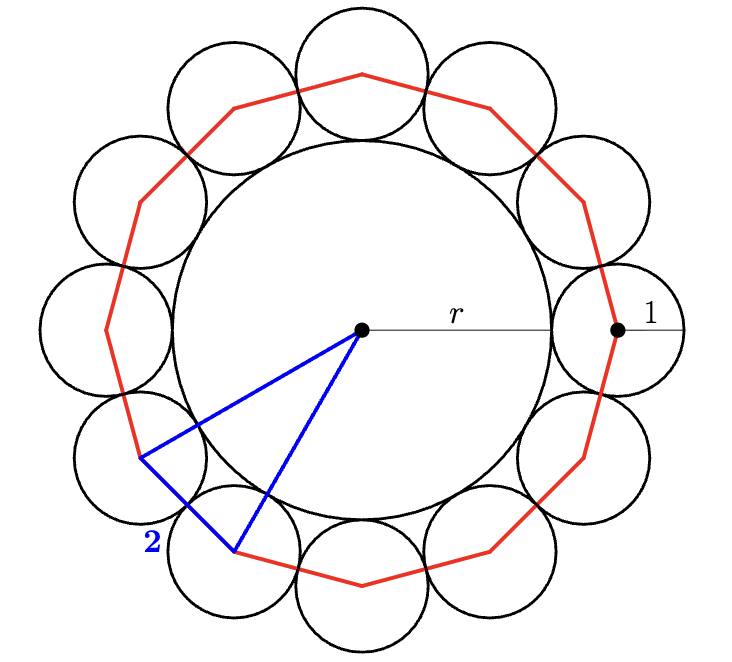
Connect the centers of the smaller circles to form a dodecagon of side length . Then, we form a triangle with base and legs . Hence:
and so . Hence, the answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions