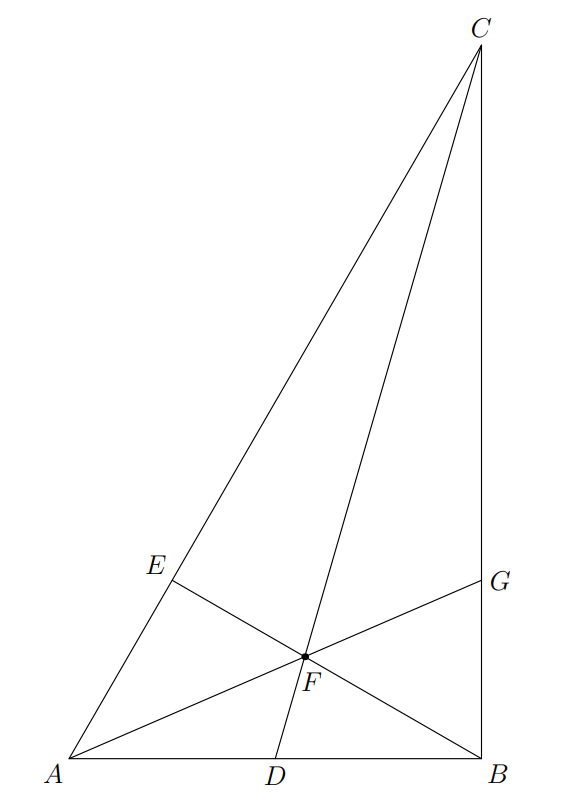
The altitude to the hypotenuse of a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ 3 0 ∘ − 6 0 ∘ − 9 0 ∘ x < y x < y x x + y ? x + y x ?
Answer Choices:
A. 3 7 7 3 3 4 4 3 4 9 9 4 5 11 1 1 5 4 3 15 1 5 4 3
💬 Join the Discussion View Forum Thread
We will use mass points.
Note that since △ A B C ∼ △ B E C △ A B C ∼ △ B E C
C E = B C 2 C A = 3 4 C E = C A B C 2 = 4 3
as △ A B C △ A B C 3 0 ∘ − 6 0 ∘ − 9 0 ∘ 3 0 ∘ − 6 0 ∘ − 9 0 ∘
Assign a mass of 3 3 A A 1 1 C C A D = D B A D = D B B B 3 3 E E 4 4 F F 7 7
Thus
F B E F = mass at E mass at B = 4 3 E F F B = mass at B mass at E = 3 4
Thus x = 3 , y = 4 x = 3 , y = 4 x x + y = (A) 3 7 x + y x = (A) 7 3
While there is a simple solution with mass points, we defer to using areas.
Note that
[ C F B ] [ C E F ] = 1 2 ⋅ F B ⋅ distance from C to F B 1 2 ⋅ E B ⋅ distance from C to E F = F B E F [ C E F ] [ C F B ] = 2 1 ⋅ E B ⋅ distance from C to E F 2 1 ⋅ F B ⋅ distance from C to F B = E F F B
as F B F B E F E F
[ C E F ] [ C A F ] = 1 2 ⋅ F E ⋅ C E 1 2 ⋅ F E ⋅ C A = C E C A [ C A F ] [ C E F ] = 2 1 ⋅ F E ⋅ C A 2 1 ⋅ F E ⋅ C E = C A C E
as F E F E A C A C
[ C A D ] = 1 2 ⋅ A D ⋅ C B = 1 2 ⋅ B D ⋅ C B = [ C B D ] [ C A D ] = 2 1 ⋅ A D ⋅ C B = 2 1 ⋅ B D ⋅ C B = [ C B D ]
[ F A D ] = 1 2 ⋅ A D ⋅ distance from F to A D = 1 2 ⋅ B D ⋅ distance from F to B D = [ F B D ] [ F A D ] = 2 1 ⋅ A D ⋅ distance from F to A D = 2 1 ⋅ B D ⋅ distance from F to B D = [ F B D ]
so [ A F C ] = [ A C D ] − [ A F D ] = [ B C D ] − [ B F C ] = [ C F B ] [ A F C ] = [ A C D ] − [ A F D ] = [ B C D ] − [ B F C ] = [ C F B ]
F B E F = [ C F B ] [ C E F ] = [ A F C ] [ C E F ] = C A C E E F F B = [ C E F ] [ C F B ] = [ C E F ] [ A F C ] = C E C A
Note that since △ A B C ∼ △ B E C △ A B C ∼ △ B E C
C E = B C 2 C A = 3 4 C E = C A B C 2 = 4 3
as △ A B C △ A B C 30 − 60 − 90 3 0 − 6 0 − 9 0
F B E F = 4 3 E F F B = 3 4
Thus x = 3 , y = 4 x = 3 , y = 4 x x + y = (A) 3 7 x + y x = (A) 7 3
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions