¶ 2025 AMC 12B Problem 15
¶ Problem:
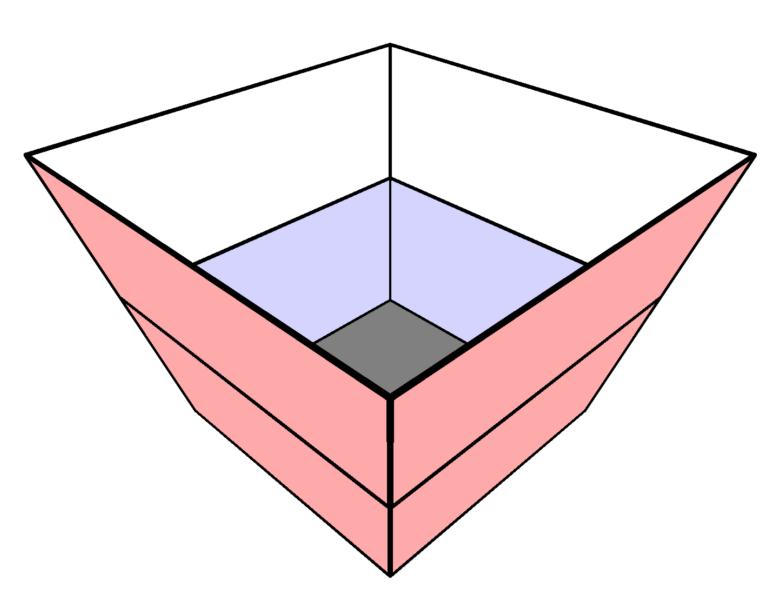
A container has a square bottom, a open square top, and four congruent trapezoidal sides, as shown. Starting when the container is empty, a hose that runs water at a constant rate takes minutes to fill the container up to the midline of the trapezoids. How many more minutes will it take to fill the remainder of the container?
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
The midlines of each trapezoid form a square with side length . Extend the legs of each trapezoidal face to meet at a point , the vertex of the formed square pyramid. Consider , , and to be square pyramids with vertex and bases as the , , and squares respectively.
Suppose the volume of is . Since , , and are similar solids, we know the ratio of their volumes is their scale factor cubed. Therefore we may say that and .
The volume of water filled so far is and the volume of water left to be filled is . Since water fills proportionally to volume, we may find the number of minutes as minutes.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions