¶ 2025 AMC 12B Problem 22
¶ Problem:
What is the greatest possible area of the triangle in the complex plane with vertices , , and , where satisfies
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
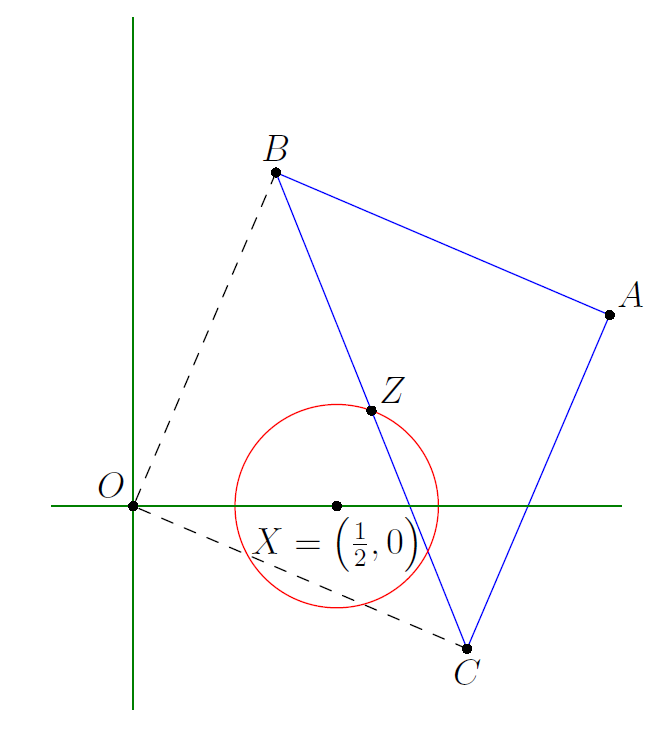
Note that represents a circle with center (denoted by point in the diagram above) and radius . Let , , and be the vertices of the triangle, and let be the origin. Then always forms a square, whose side length is always . Hence, the area of the triangle is always equal to .
To maximize this area, it is sufficient to maximize i.e. maximize . Since , the maximum possible area is , which corresponds to .
Alternate Solution:
Consider the triangle with vertices , , and , with area . Then the triangle with vertices , , and is a transformation of the original triangle, where we dilate it by a factor of and rotate it counterclockwise by an angle of . Hence, by similar triangles, its new area is . The rest of the solution follows as above.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions