¶ 2025 AMC 12B Problem 24
¶ Problem:
How many real numbers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
We must have that , so . The period of is , so in the range , the sine curve has full periods of the form for .
Note that in each period, there are two distinct intersections. This includes the final period, since at , the log curve is at , while the sine curve is at i.e. the situation as follows:
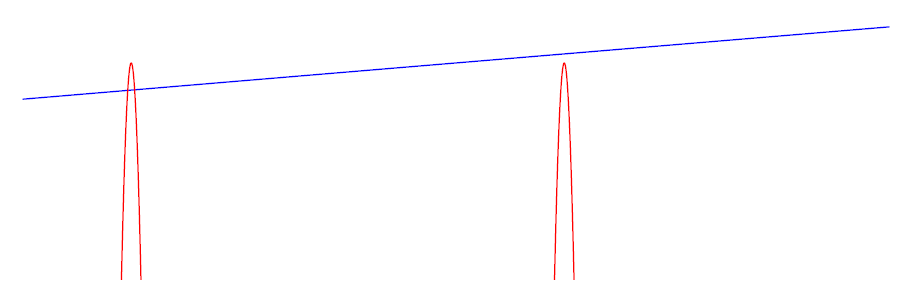
However, one of the intersections (namely ) is a part of two different periods, and so it is double-counted, as shown below.
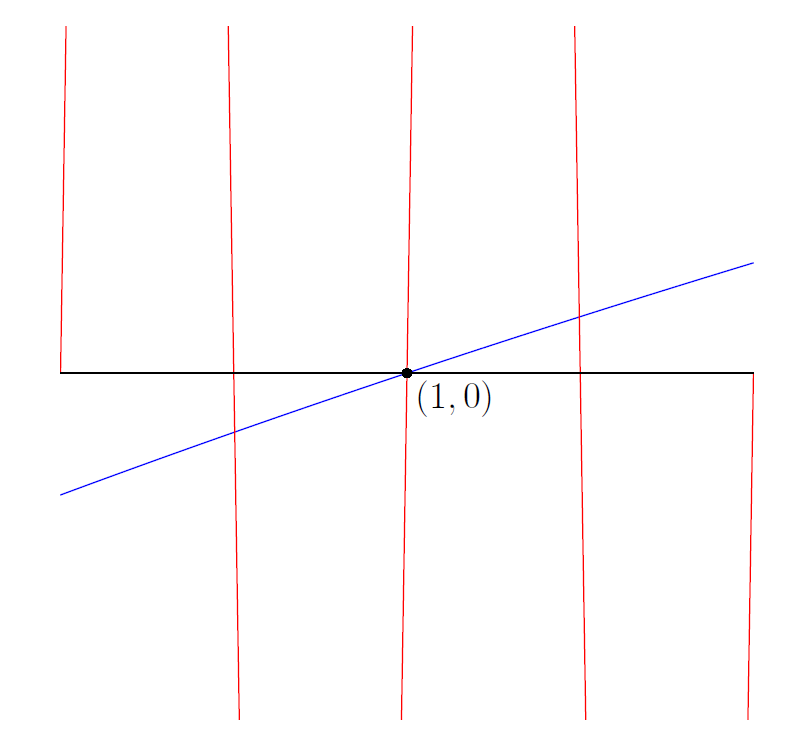
Hence, the total number of intersection points if , which corresponds to .
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions