¶ 2025 AMC 12B Problem 25
¶ Problem:
Three concentric circles have radii . An equilateral triangle with side length has one vertex on each circle. What is
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
Suppose , , and are the vertices of the equilateral triangle on the circles of radius , , and , and suppose that point is the center of the concentric circles, so that our diagram is as follows:
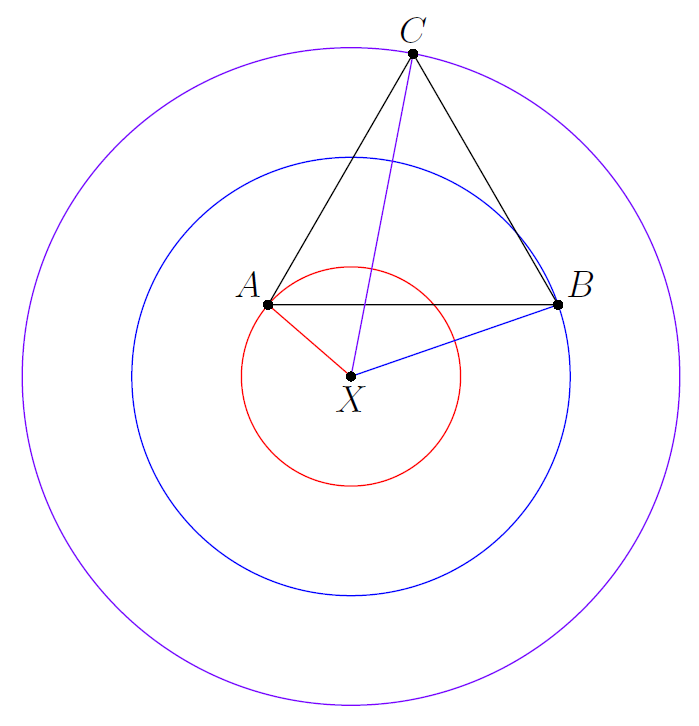
Since , we must have that lies on the circumcircle of , by the converse of Ptolemy's theorem. This is depicted below.
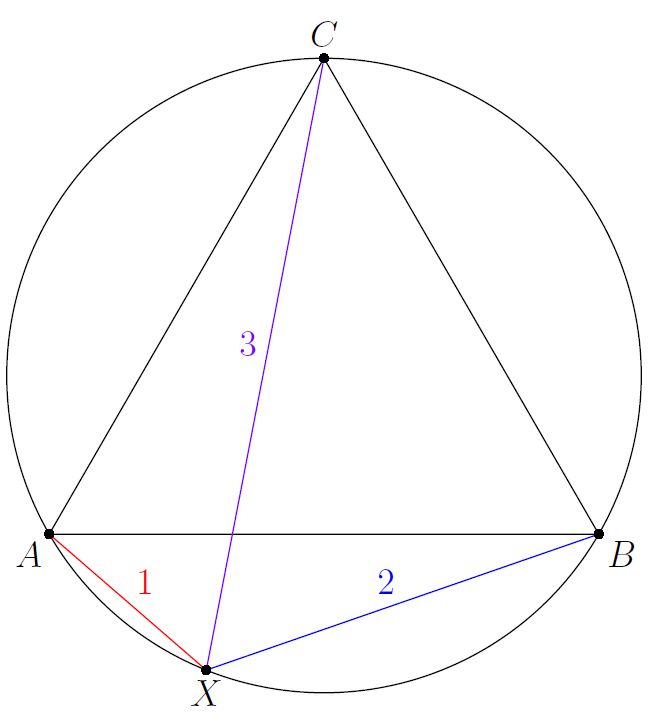
Hence, . Since and , we have that:
by Law of Cosines, so the answer is .
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions