Problem:
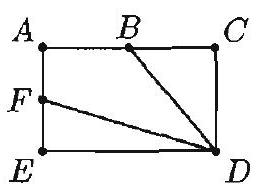
The rectangle shown has length AC=32, width AE=20, and B and F are midpoints of AC and AE, respectively. The area of the quadrilateral ABDF is
Answer Choices:
A. 320
B. 325
C. 330
D. 335
E. 340
Solution:
Rectangle ACDE has area 32Γ20=640. Triangle BCD has area (16Γ20)/2=160, and triangle DEF has area (10Γ32)/2=160. The remaining area, ABDF, is 640β(160+160)=320.
OR
Insert diagonal AD. The areas of triangles ABD and BCD are (AB)(CD)/2 and (BC)(CD)/2 which are equal since AB=BC. Hence half the area in the rectangle above AΛDΛ is in ABDF. Similarly, triangles ADF and DEF have equal areas, and half the area in the rectangle below AD is in ABDF. Thus, the area of ABDF is (32Γ20)/2=320.
OR
Draw a perpendicular from point B to ED to show that the area of β³BCD is one fourth of the area of ACDE.
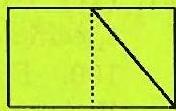
Similarly, draw a perpendicular from point F to CD to show that the area of β³DEF is one fourth of the area of ACDE. Thus the area of ABDF is one half of the area of ACDE, or (32Γ20)/2=320.
Answer: Aβ.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)
.jpg)