¶ 1994 AMC8 Problem 12
Problem:
Each of the three large squares shown below is the same size. Segments that intersect the sides of the squares intersect at the midpoints of the sides. How do the shaded areas of these squares compare?
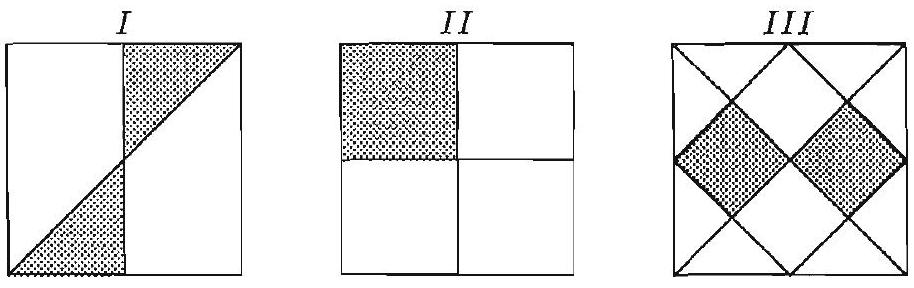
Answer Choices:
A. The shaded areas in all three are equal.
B. Only the shaded areas of and are equal.
C. Only the shaded areas of and are equal.
D. Only the shaded areas of and are equal.
E. The shaded areas of and are all different.
Solution:
The shaded area of square is clearly of the total area. In square each shaded triangle is of or of the total area, so the total shaded area is of the total. In square , each shaded diamond can be visualized as two triangles. Each of these triangles is of or of the total area, so the four triangles make up or of the total. Thus the shaded areas in all three are equal.
Partition the squares to note that of congruent triangles are shaded in , that of congruent small squares is shaded in and that of congruent triangles are shaded in .
.jpg)
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions